6.tìm số đo x ở các hình 55,56,57,58

Những câu hỏi liên quan
Tìm số đo x ở các hình 55, 56, 57, 58.
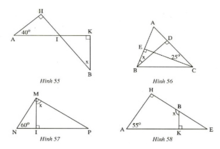
Áp dụng tính chất “Trong tam giác vuông, hai góc nhọn phụ nhau” ta có:
+ Hình 55:

+ Hình 56:

+ Hình 57 :

+ Hình 58:
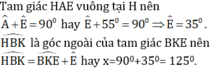
Đúng 0
Bình luận (0)
Tìm số đo x ở hình bên là
Đọc tiếp
Tìm số đo x ở hình bên là
Xét tứ giác MNPQ: \(x+2x+3x+4x=360^0\)
\(\Rightarrow10x=360^0\\ \Rightarrow x=36^0\)
Đúng 3
Bình luận (0)
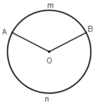
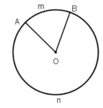
Trên các hình 5, 6 hãy dùng dụng cụ đo góc để tìm số đo cung AmB.
Từ đó, tính số đo cung AnB tương ứng.
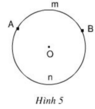
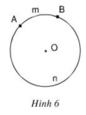
Trên các hình 5, 6 hãy dùng dụng cụ đo góc để tìm số đo cung AmB.
Từ đó, tính số đo cung AnB tương ứng.

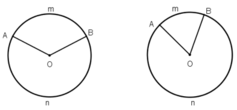
Kiến thức áp dụng
+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+ Số đo của cung lớn bằng hiệu của 360º và số đo của cung nhỏ (có chung hai mút với cung lớn).
Đúng 0
Bình luận (0)
Tính các số đo x, y ở các hình 47, 48, 49, 50, 51.
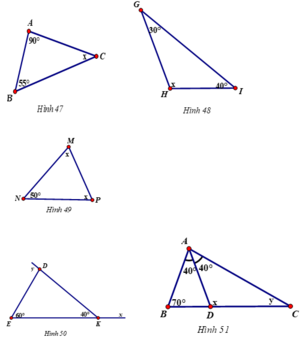
Áp dụng định lý tổng ba góc trong một tam giác bằng 180º ta có:
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
Áp dụng định lý góc ngoài của tam giác ta có:
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
- Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70º + 40º = 110º
Áp dụng định lý tổng ba góc trong tam giác ADC có:
y + 110º + 40º = 180º ⇒ y = 30º.
Đúng 0
Bình luận (0)
Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

Do tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
\(130^\circ + \widehat B + 60^\circ + \widehat D = 360^\circ \)
\(\widehat B + \widehat D = 170^\circ \) (1)
Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AC\) (gt)
\(BC = DC\) (gt)
\(AC\) chung
\( \Rightarrow \Delta ABC = \Delta ADC\) (c-c-c)
\( \Rightarrow \widehat B = \widehat D\) (hai góc tương ứng) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat D = \frac{{170^\circ }}{2} = 85^\circ \)
Đúng 0
Bình luận (0)
Tìm số đo góc x ở hình bên:A. 30o B.50oC.90o D.130o
Đọc tiếp
Tìm số đo góc x ở hình bên:
A. 30o B.50o
C.90o D.130o
Tìm các số đo x, y trong Hình 140.

Tam giác ABO là tam giác đều nên \(\widehat {ABO} = \widehat {AOB} = \widehat {BAO} = 60^\circ \). Vậy \(x = 60^\circ \).
Ba điểm B, O, C thẳng hàng nên \(\widehat {BOC} = 180^\circ \). Mà \(\widehat {AOB} = 60^\circ \)nên \(\widehat {AOC} = 180^\circ - 60^\circ = 120^\circ \).
Xét tam giác AOC có OA = OC. Vậy tam giác AOC cân tại O nên \(\widehat{OAC} = \widehat{OCA} =\dfrac{1}{2}. (180^0-\widehat{AOC})= \dfrac{1}{2}.(180^\circ - 120^\circ ) = 30^\circ \)
Hay \(y = 30^\circ \).
Vậy \(x = 60^\circ \); \(y = 30^\circ \).
Đúng 0
Bình luận (0)
Bài 1: Tìm số đo x trong các hình sau, biết AB//CD.
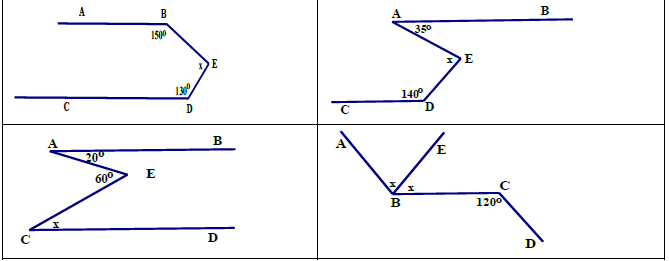
\(x=80^o\) \(x=75^o\)
\(x=20^o\) \(x=60^o\)
Đúng 0
Bình luận (1)