Cho đường tròn (C) có phương trình: x − 1 2 + y + 1 2 = 4 . Viết phương trình đường tròn (C’) là ảnh của (C) qua phép đối xứng qua trục Oy.
A. x + 1 2 + y + 1 2 = 4
B. x − 1 2 + y + 1 2 = 4
C. x + 1 2 + y − 1 2 = 4
D. x − 1 2 + y − 1 2 = 4
Những câu hỏi liên quan
Trong mặt phẳng Oxy,cho đường tròn (C) có phương trình (x-3)2+(y+1)2=10.Viết phương trình tiếp tuyến cua đường tròn đã cho tại điểm M∈(C),biết hoành độ của điểm M là X0=2
+
Gọi \(M\left(2;y_M\right)\) là tiếp điểm của (C):
\(\Leftrightarrow2^2+y_M^2-12+2y_M=0\)
\(\Leftrightarrow y_M^2+2y_M-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y_M=2\\y_M=-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}M\left(2;2\right)\\M\left(2;-4\right)\end{matrix}\right.\)
* Với M(2;2)
Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;3\right)\Rightarrow\overrightarrow{n}=\left(3;1\right)\)
\(\Rightarrow\left(D\right):3x+y-8=0\)
* Với M(2; -4)
Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;-3\right)\Rightarrow\overrightarrow{n}=\left(-3;1\right)\)
\(\Rightarrow\left(D\right):-3x+y+4=0\)
Đúng 2
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình:
x
−
3
2
+
y
+
1
2
9
.Hãy viết phương trình của đường tròn (C’)...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình: x − 3 2 + y + 1 2 = 9 .
Hãy viết phương trình của đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I(1; 2) tỉ số k = -2
Ta có A(3;−1) là tâm của (C) nên tâm A' của (C') là ảnh của A qua phép vị tự đã cho. Từ đó suy ra A′ = (−3;8). Vì bán kính của (C) bằng 3, nên bán kính của (C') bằng |−2|.3 = 6
Vậy (C') có phương trình: x + 3 2 + y − 8 2 = 36 .
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:
x
-
1
2
+
y
-
2
2
4
. Hỏi phép vị tự tâm O tỉ số k -2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau? A....
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: x - 1 2 + y - 2 2 = 4 . Hỏi phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x - 2 2 + y - 4 2 = 4
B. x + 2 2 + y + 4 2 = 4
C. x - 2 2 + y - 4 2 = 16
D. x + 2 2 + y + 4 2 = 16
Tìm tâm và bán kính của đường tròn trong môi trường hợp sau:
a) Đường tròn có phương trình\({(x + 1)^2} + {(y - 5)^2} = 9\) ;
b) Đường tròn có phương trình\({x^2} + {y^2}-6x - 2y-{\rm{1}}5 = 0\) .
a) Đường tròn \({(x + 1)^2} + {(y - 5)^2} = 9\) có tâm \(I\left( { - 1;5} \right)\) và \(R = 3\)
b) Đường tròn \({x^2} + {y^2}-6x - 2y-{\rm{1}}5 = 0\) có tâm \(I\left( {3;1} \right)\) và \(R = \sqrt {{3^2} + {1^2} + 15} = 5\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường tròn (C):
(
x
+
1
)
2
+
(
y
-
3
)
2
4
. Phép tịnh tiến theo véc tơ
v
⇀
(
3
;
2
)
biến đường tròn (C) t...
Đọc tiếp
Trong mặt phẳng Oxy, cho đường tròn (C): ( x + 1 ) 2 + ( y - 3 ) 2 = 4 . Phép tịnh tiến theo véc tơ v ⇀ = ( 3 ; 2 ) biến đường tròn (C) thành đường tròn có phương trình nào sau đây?
A. x - 1 2 + y + 3 2 = 4
B. x + 2 2 + y + 5 2 = 4
C. x - 2 2 + y - 5 2 = 4
D. x + 4 2 + y - 1 2 = 4
Trong mặt phẳng tọa độ oxy, cho đường tròn C phương trình là : C x^2 + y^2 =1. đường tròn C' tâm I(2,2) cắt C tại A,B sao cho AB = √2. viết phương trình đường thẳng AB.
Đường tròn (C) tâm O(0;0) bán kính R=1
Phương trình đường thẳng IO có dạng: \(y=x\)
Do A;B là giao điểm của 2 đường tròn \(\Rightarrow AB\perp IO\)
Gọi H là trung điểm AB \(\Rightarrow H\in OI\) ; \(AH=\dfrac{AB}{2}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow OH=\sqrt{OA^2-AH^2}=\sqrt{1-\dfrac{1}{2}}=\dfrac{\sqrt{2}}{2}\)
Do H thuộc OI nên tọa độ có dạng: \(H\left(x;x\right)\Rightarrow OH=\sqrt{x^2+x^2}=\sqrt{2x^2}\)
\(\Rightarrow\sqrt{2x^2}=\dfrac{\sqrt{2}}{2}\Rightarrow x=\pm\dfrac{1}{2}\) \(\Rightarrow\left[{}\begin{matrix}H\left(\dfrac{1}{2};\dfrac{1}{2}\right)\\H\left(-\dfrac{1}{2};-\dfrac{1}{2}\right)\end{matrix}\right.\)
Đường thẳng AB qua H và vuông góc OI nên nhận \(\left(1;1\right)\) là 1 vtpt có dạng:
\(\left[{}\begin{matrix}1\left(x-\dfrac{1}{2}\right)+1\left(y-\dfrac{1}{2}\right)=0\\1\left(x+\dfrac{1}{2}\right)+1\left(y+\dfrac{1}{2}\right)=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+y-1=0\\x+y+1=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong hệ trục tọa đô Oxy. Cho đường tròn (C):(x-1)2+(y-2)2=5
a/Viết phương trình đường thẳng (d) đi qua gốc tọa đố và tâm của đường tròn (C)
b/Viết phương trình đường thẳng(Δ) đi qua M(1;3) cắt đường tròn (C) theo dây cung AB có độ dài bằng \(3\sqrt{2}\)
làm nhanh giúp e vs ạ
Đường tròn (C) tâm I(1;2) bán kính \(R=\sqrt{5}\)
a.
\(\overrightarrow{OI}=\left(1;2\right)\Rightarrow\) đường thẳng OI nhận (2;-1) là 1 vtpt
Phương trình: \(2\left(x-0\right)-1\left(y-0\right)=0\Leftrightarrow2x-y=0\)
b.
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\Rightarrow IH=d\left(I;\Delta\right)\)
Áp dụng định lý Pitago:
\(IH=\sqrt{IA^2-AH^2}=\sqrt{R^2-\left(\dfrac{AB}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
Phương trình \(\Delta\) qua M có dạng:
\(a\left(x-1\right)+b\left(y-3\right)=0\) với \(a^2+b^2>0\)
\(d\left(I;\Delta\right)=\dfrac{\left|a\left(1-1\right)+b\left(2-3\right)\right|}{\sqrt{a^2+b^2}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left|\sqrt{2}b\right|=\sqrt{a^2+b^2}\Leftrightarrow2b^2=a^2+b^2\)
\(\Leftrightarrow a^2=b^2\Leftrightarrow\left[{}\begin{matrix}a=b\\a=-b\end{matrix}\right.\)
Chọn \(a=1\Rightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(1;1\right)\\\left(a;b\right)=\left(1;-1\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}1\left(x-1\right)+1\left(y-3\right)=0\\1\left(x-1\right)-1\left(y-3\right)=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;-3) tỉ số k 1/2, biến đường tròn (C) có phương trình :
x
-
2
2
+
y
-
3
2
32
thành đường tròn (C’) có phương trình: A....
Đọc tiếp
Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;-3) tỉ số k = 1/2, biến đường tròn (C) có phương trình : x - 2 2 + y - 3 2 = 32 thành đường tròn (C’) có phương trình:
A. x - 3 / 2 2 + y 2 = 16
B. x - 3 / 2 2 + y - 2 2 = 8
C. x - 3 2 + y - 2 2 = 32
D. x - 3 / 2 2 + y 2 = 8
Phép vị tự tâm H (1; -3) tỉ số k = 1/2, biến tâm I(2; 3) của (C) thành I’(x; y)
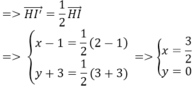
biến bán kính R = 4√2 thành R' = 2√2 ⇒ phương trình (C’) là:
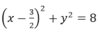
Đáp án D
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình
x
-
1
2
+
y
-
1
2
4
Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k2 biến (C) thành đường tròn nào trong các đường t...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x - 1 2 + y - 1 2 = 4 Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k=2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x - 1 2 + y - 2 2 = 8
B. x - 2 2 + y - 2 2 = 8
C. x + 2 2 + y + 2 2 = 16
D. x - 1 2 + y - 2 2 = 16
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình
x
−
1
2
+
y
−
1
2
4.
Phép vị tự tâm O (với O là gốc tọa độ) tỉ số
k
2
biến (C) thành đường tròn nào trong các đường tròn có phương trình sau? A. ...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x − 1 2 + y − 1 2 = 4. Phép vị tự tâm O (với O là gốc tọa độ) tỉ số k = 2 biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?
A. x − 1 2 + y − 1 2 = 8.
B. x − 2 2 + y − 2 2 = 8.
C. x + 2 2 + y + 2 2 = 16.
D. x − 2 2 + y − 2 2 = 16.
Đáp án D
(C) có tâm I(1;1)và bán kính R = 2
Giả sử V 2 O : C → C ' , trong đó (C')có tâm I ' a ; b , bán kính R'
Ta có: a = 2.1 = 2 b = 2.1 = 2 ⇒ I ' 2 ; 2 và R ' = 2.2 = 4 ⇒ C ' : x − 2 2 + y − 2 2 = 16
Đúng 0
Bình luận (0)