Ta có yêu cầu bài toán tương đương với:

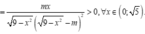
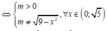
Vậy có tất cả 7 số nguyên thoả mãn.

Chọn đáp án B.

Chọn đáp án B.

Ta có yêu cầu bài toán tương đương với

y ' = m x 9 - x 2 ( 9 - x 2 - m ) 2 > 0 , ∀ x ∈ 0 ; 5

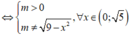
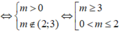
Vậy có tất cả 7 số nguyên thoả mãn.

\(2^x=t\Rightarrow t\in\left(1;4\right)\)

\(t^2-2m.t+9=0\)

\(\Leftrightarrow m=\dfrac{t^2+9}{2t}\)

Xét \(f\left(t\right)=\dfrac{t^2+9}{2t}\) trên (1;4),

 \(f\left(1\right)=5\) ; \(f\left(4\right)=\dfrac{25}{8}\) ; \(f\left(t\right)=\dfrac{t^2+9}{2t}\ge\dfrac{6t}{2t}=3\)

\(\Rightarrow f\left(t\right)\) có 2 nghiệm khi \(3< m< \dfrac{25}{8}\) và có 1 nghiệm khi \(\dfrac{25}{8}\le m< 5\)

Có 1 giá trị m

Chà câu kia mỏi cổ quá:

Nhân 2 vế với \(3^{6\sqrt{x}-1}\) và rút gọn:

\(3^{\dfrac{3}{x}+6\sqrt{x}}-3.3^{\dfrac{2}{x}+2\sqrt{x}}+\left(m+2\right)3^{\dfrac{1}{x}+2\sqrt{x}}-m=0\)

\(\Leftrightarrow\left(3^{\dfrac{1}{x}+2\sqrt{x}}\right)^3-3.\left(3^{\dfrac{1}{x}+2\sqrt{x}}\right)^2+\left(m+2\right).3^{\dfrac{1}{x}+2\sqrt{x}}-m=0\)

\(\dfrac{1}{x}+2\sqrt{x}=\dfrac{1}{x}+\sqrt{x}+\sqrt{x}\ge3\sqrt[3]{\dfrac{x}{x}}=3\)

Do đó đặt \(3^{\dfrac{1}{x}+2\sqrt{x}}=t\Rightarrow t\ge3^3=27\)

\(\Rightarrow t^3-3t^2+\left(m+2\right)t-m=0\)

\(\Leftrightarrow\left(t-1\right)\left(t^2-2t+m\right)=0\)

\(\Leftrightarrow t^2-2t+m=0\)

\(\Leftrightarrow m=-t^2+2t\)

Xét hàm \(f\left(t\right)=-t^2+2t\) với \(t\ge27\), từ BBT dễ dàng suy ra \(m\le f\left(27\right)=-675\)

Đáp án B

Phương trình đã cho tương đương với: x ≥ 2 2 x 2 − x − 2 m = x 2 − 4 x + 4 ⇔ x ≥ 2 x 2 + 3 x − 4 = 2 m

Xét hàm  y = x 2 + 3 x − 4 trên 2 ; + ∞  ta có

BBT:

Để phương trình đã cho có nghiệm điều kiện là  2 m ≥ 6 ⇔ m ≥ 3

Mà  m ∈ [ - 2017 ; 2017 )  suy ra  3 ≤ m < 2017

Vậy có nhiều nhất 2014 số nguyên thỏa mãn yêu cầu bài toán.

Đáp án cần chọn là: A

Ta có:

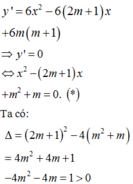
⇒ *  luôn có hai nghiệm phân biệt x 1 ; x 2 x 1 < x 2  với mọi m.

Áp dụng hệ thức Vi-ét ta có:

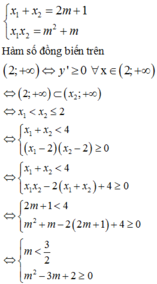
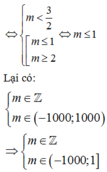
Vậy có tất cả 1001 giá trị m thỏa mãn bài toán.

Chọn B.

Chọn B

Phương pháp:

Tính y'.

Tìm m để 

Cách giải:

Ta có 

Xét phương trình y' = 0  có 

Suy ra phương trình y' = 0 luôn có hai nghiệm 

Dễ thấy  trong khoảng  thì hàm số đồng biến.

Bài toán thỏa 

Do 

Vậy có  giá trị của m thỏa mãn bài toán.

Chú ý:

Cách khác: Tìm m để 

Theo định lí Viet, ta có 

Hàm số đồng biến trên  ( 2 ; + ∞ )   ⇔   phương trình y' = 0 có hai nghiệm 

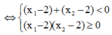
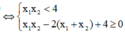
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)