Question

Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng (-10000;10000) để hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2   +   6 m ( m + 1 ) x   +   1  đồng biến trên khoảng ( 2 ; + ∞ ) ?

A. 999.

B. 1001.

C. 1998.

D. 1000.

Answer 1

Chọn B

Phương pháp:

Tính y'.

Tìm m để 

Cách giải:

Ta có 

Xét phương trình y' = 0  có 

Suy ra phương trình y' = 0 luôn có hai nghiệm 

Dễ thấy  trong khoảng  thì hàm số đồng biến.

Bài toán thỏa 

Do 

 

Vậy có  giá trị của m thỏa mãn bài toán.

Chú ý:

Cách khác: Tìm m để 

Theo định lí Viet, ta có 

Hàm số đồng biến trên  ( 2 ; + ∞ )   ⇔   phương trình y' = 0 có hai nghiệm 

 

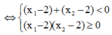
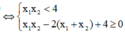
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)