Tập xác định của phương trình 2 x x 2 + 1 - 5 = 3 x 2 + 1 là
A. D = ℝ \ 1
B. D = ℝ \ - 1
C. D = ℝ \ ± 1
D. D = ℝ
Những câu hỏi liên quan
Cho bất phương trình
x
+
1
(
x
-
2
)
2
x
+
1
. Tập xác định của bất phương trình là: A. [-1;
+
∞
] B. (-1;
+...
Đọc tiếp
Cho bất phương trình x + 1 ( x - 2 ) 2 < x + 1 . Tập xác định của bất phương trình là:
A. [-1; + ∞ ]
B. (-1; + ∞ )
C. x ≥ -1, x ≠ 2
D. [-1;2) ∪ (2; + ∞ )
Đáp án: D
x + 1 ( x - 2 ) 2 < x + 1
ĐKXĐ: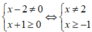 
Vậy tập xác định của bất phương trình là: [-1;2) ∪ (2; + ∞ )
Chú ý: Học sinh thường hay nhầm lẫn giữa đáp án C và D. Khi câu hỏi là “tập xác định” thì chúng ta phải biểu diễn kết quả dưới dạng tập hợp như đáp án D
Đúng 0
Bình luận (0)
Cho phương trình
x
2
+
x
+
1
x
-
3
1
x
-
2
Tập xác định của phương trình là: A.
[
2
;
+
∞
)
B.
[
0
;
+
∞
)
C.
[...
Đọc tiếp
Cho phương trình x 2 + x + 1 x - 3 = 1 x - 2 Tập xác định của phương trình là:
A. [ 2 ; + ∞ )
B. [ 0 ; + ∞ )
C. [ 0 ; + ∞ ) / 3
D. [ 2 ; + ∞ ) \ 3
Giải mục 1 trang 35 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 20:12
Xác định và so sánh tập nghiệm của các phương trình sau:
\(\begin{array}{l}a)\;x - 1 = 0\\b)\;{x^2} - 1 = 0\\c)\sqrt {2{x^2} - 1} = x\end{array}\)
\(a,x-1=0\Leftrightarrow x=1\)
Vậy tập nghiệm của phương trình là \(S=\left\{1\right\}\)
\(b,x^2-1=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là \(S=\left\{-1;1\right\}\)
c, ĐK: \(x\ge\dfrac{\sqrt{2}}{2}\)
\(\sqrt{2x^2-1}=x\Leftrightarrow2x^2-1=x^2\Leftrightarrow x^2=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là \(S=\left\{-1;1\right\}\)
Từ đó, hai phương trình b và c có cùng tập nghiệm.
Đúng 0
Bình luận (0)
Điều kiện xác định của phương trình
x
-
2
+
6
x
-
3
4
là tập nào sau đây? A.
R
3
.
B....
Đọc tiếp
Điều kiện xác định của phương trình x - 2 + 6 x - 3 = 4 là tập nào sau đây?
A. R \ 3 .
B. 2 ; + ∞ .
C.R
D. 2 ; + ∞ \ 3 .
Tập xác định của phương trình
3
x
+
5
x
2
+
1
2
2
−
x
là: A.
D
−
5
3...
Đọc tiếp
Tập xác định của phương trình 3 x + 5 x 2 + 1 = 2 2 − x là:
A. D = − 5 3 ; 2
B. D = − 5 3 ; 2
C. D = − 5 3 ; 2
Điều kiện xác định 3 x + 5 ≥ 0 2 − x > 0 ⇔ x ≥ − 5 3 x < 2 ⇔ − 5 3 ≤ x < 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Bài 1: Cho bất phương trình \(4\sqrt{\left(x+1\right)\left(3-x\right)}\le x^2-2x+m-3\). Xác định m để bất phương trình nghiệm \(\forall x\in[-1;3]\)
Bài 2: Cho bất phương trình \(x^2-6x+\sqrt{-x^2+6x-8}+m-1\ge0\). Xác định m để bất phương trình nghiệm đúng \(\forall x\in[2;4]\)
Câu 3. Phương trình vô nghiệm có tập nghiệm là?A. S f B. S 0 C. S {0} D. S {f}Câu 4. Điều kiện xác định của phương trình là?A. x ≠ 2 và B. x ≠ -2 và C. x ≠ -2 và x ≠ 3 D. x ≠ 2 và Câu 5. Cho AB 3cm, CD 40cm. Tỉ số của hai đoạn thẳng AB và CD bằng?A. B. C. D.
Đọc tiếp
Câu 3. Phương trình vô nghiệm có tập nghiệm là?
A. S = f B. S = 0 C. S = {0} D. S = {f}
Câu 4. Điều kiện xác định của phương trình là?
A. x ≠ 2 và B. x ≠ -2 và C. x ≠ -2 và x ≠ 3 D. x ≠ 2 và
Câu 5. Cho AB = 3cm, CD = 40cm. Tỉ số của hai đoạn thẳng AB và CD bằng?
A. B. C. D.
Tập xác định của phương trình
x
-
5
5
-
x
là: A.
[
5
;
+
∞
)
B.
(
-
∞
;
5
]
C.
-
5
;
5
D.
5
Đọc tiếp
Tập xác định của phương trình x - 5 = 5 - x là:
A. [ 5 ; + ∞ )
B. ( - ∞ ; 5 ]
C. - 5 ; 5
D. 5
Điều kiện xác định của phương trình : x - 5 ≥ 0 5 - x ≥ 0 ⇔ x ≥ 5 x ≤ 5 ⇔ x = 5
Do đó, tập xác định của phương trình là D= {5}
Đúng 0
Bình luận (0)
1.Tập các giá trị nguyên của x để biểu thức \(\sqrt{x-1}-\frac{x}{\sqrt{1-x}}\) xác định.
2.Tập nghiệm nguyên của bất phương trình: \(\sqrt{5x-2}\le4\).
Cho phương trình :x^2-2left(m-1right)x+m^2-3m0a) Xác định m để phương trình có 2 nghiệm phân biệtb) Xác định m để phương trình có đúng 1 nghiệm âmc) Xác định m để phương trình có 1 nghiệm bằng 0. Tìm nghiệm còn lạid) Tìm hệ thức liên hệ giữa 2 nghiệm x1, x2 của phương trình không phụ thuộc và me) Xác định m để phương trình có 2 nghiệm thỏa mãn x1^2+x2^28
Đọc tiếp
Cho phương trình :
\(x^2-2\left(m-1\right)x+m^2-3m=0\)
a) Xác định m để phương trình có 2 nghiệm phân biệt
b) Xác định m để phương trình có đúng 1 nghiệm âm
c) Xác định m để phương trình có 1 nghiệm bằng 0. Tìm nghiệm còn lại
d) Tìm hệ thức liên hệ giữa 2 nghiệm x1, x2 của phương trình không phụ thuộc và m
e) Xác định m để phương trình có 2 nghiệm thỏa mãn \(x1^2+x2^2=8\)
x2-2(m-1)x+m2-3m=0
△'=[-(m-1)]2-1(m2-3m)=(m-1)2-(m2-3m)=m2-2m+1-m2+3m= m+1
áp dụng hệ thức Vi-ét ta được
x1+x2=2(m-1) (1)
x1*x2=m2-3m (2)
a) để PT có 2 nghiệm phân biệt khi m+1>0 <=> m>-1
b) để PT có duy nhất một nghiệm âm thì x1*x2 <0
Đúng 0
Bình luận (0)
e) Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1x_2=m^2-3m\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\)
\(\Leftrightarrow\left(2m-2\right)^2-2\cdot\left(m^2-3m\right)-8=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+6m-8=0\)
\(\Leftrightarrow2m^2-2m-4=0\)(1)
\(\Delta=\left(-2\right)^2-4\cdot2\cdot\left(-4\right)=4+32=36\)
Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{2-\sqrt{36}}{4}=\dfrac{2-6}{4}=-1\\m_2=\dfrac{2+\sqrt{36}}{4}=\dfrac{2+6}{4}=2\end{matrix}\right.\)
Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2=8\) thì \(m\in\left\{-1;2\right\}\)
Đúng 1
Bình luận (0)