Cho các hàm số f x = x + 1 x 2 + x - 6 và g x = tan x + sin x
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm liên tục.
Bải 1: Tìm tập xác định của các hàm số
sau:
a)
3x-2
2x+1
c) y=\sqrt{2x+1}-\sqrt{3-x}
b) y=
²+2x-3
d) y=
√2x+1
X
f(x)
Chú ý: * Hàm số cho dạng v
thi f(x) * 0.
ở Hàm số cho dạng y = v/(x) thì f(r) 2 0.
X
* Hàm số cho dạng " J7(p) thi f(x)>0.
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
Cho hàm số y=f(x). Đồ thị hàm số y=f '(x) như hình vẽ

Hàm số g(x)=f(1-2x) đồng biến trên khoảng nào trong các khoảng sau?
A. - 1 ; 0
B. - ∞ ; 0
C. 0 ; 1
D. 1 ; + ∞
1, Cho hàm số y=f(x) và f'(0)=3. Hỏi giới hạn \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}\)=?
2, Cho hàm số f(x) có đạo hàm trên R và f'(x)=0 có các nghiệm là 1 và -2. Đặt \(g\left(x\right)=f\left(\sqrt{x^2+4}\right)\), hỏi g'(x)=0 có bao nhiêu nghiệm?
Mọi người giúp mình với ạ, mình cần gấp!! Cảm ơn mọi người rất nhiều!!!
1. Áp dụng quy tắc L'Hopital
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)
2.
\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\)
2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm
Cho hàm số f(x) thỏa mãn f'(x) + 2x f(x) = 2 xe - x 2 và f(0)=1. Tất cả các nguyên hàm của x f x e x 2 là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: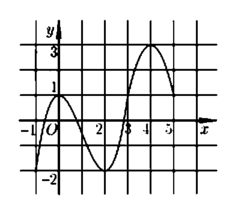
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Đáp án D
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.
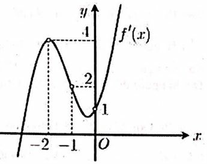
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số f(x)=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
a) Tìm các g/trị của x để hàm số xác định
b) Tính f(\(4-2\sqrt{3}\)) và f(\(a^2\)) với a< -1
c) Tìm x sao cho f(x)=f(\(x^2\))
Cho hàm số y=f(x) có đồ thị hàm số y=f’(x) như hình bên dưới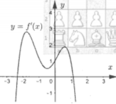
Hàm số g(x)=f(1-4x) đồng biến trên khoảng nào trong các khoảng sau?
![]()
![]()
![]()
Cho hàm số y= f(x) . Đồ thị hàm số y= f’(x) như hình bên. Hỏi hàm số y= g(x) = f(1-x2) nghịch biến trên khoảng nào trong các khoảng sau?
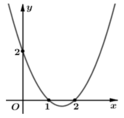
A. (1; 2)
B. (0; + ∞)
C. (-2; -1)
D. (-1; 1)
Cho hàm số f(x) có đạo hàm f'(x) thỏa mãn các đẳng thức ∫ 0 1 ( 2 x - 1 ) f ' ( x ) d x = 10 , f ( 1 ) + f ( 8 ) = 0 . Tính I = ∫ 0 1 f ( x ) d x .
A. I = 2.
B. I = 1.
C. I = -1.
D. I = -2.