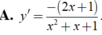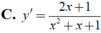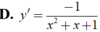Đạo hàm của hàm số
y
ln
(
1
-
x
2
)
là
Đọc tiếp
Đạo hàm của hàm số y = ln ( 1 - x 2 ) là
Những câu hỏi liên quan
Đạo hàm của hàmĐạo hàm của hàm số y (2x+1)ln(1-x) là số y (2x+1)ln(1-x) là
Đọc tiếp
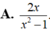
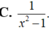
Đạo hàm của hàmĐạo hàm của hàm số y = (2x+1)ln(1-x) là số y = (2x+1)ln(1-x) là
Đạo hàm của hàm số
y
x
+
2
x
-
1
ln
(
x
+
2
)
là A.
y
2
x
log
(...
Đọc tiếp
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
25 tháng 11 2023 lúc 10:53
Tính đạo hàm của các hàm số sau:
g) \(y = \ln (x^2+x+1)\)
l) \(y = \dfrac{\ln x}{x+1}\)
g: \(y=ln\left(x^2+x+1\right)\)
=>\(y'=\dfrac{\left(x^2+x+1\right)'}{x^2+x+1}=\dfrac{2x+1}{x^2+x+1}\)
l: \(y=\dfrac{lnx}{x+1}\)
=>\(y'=\dfrac{\left(lnx\right)'\cdot\left(x+1\right)-\left(x+1\right)'\left(lnx\right)}{\left(x+1\right)^2}\)
=>\(y'=\dfrac{\dfrac{1}{x}\left(x+1\right)-lnx}{\left(x+1\right)^2}\)
\(\Leftrightarrow y'=\dfrac{\dfrac{\left(x+1\right)}{x}-lnx}{\left(x+1\right)^2}\)
Đúng 2
Bình luận (0)
Đạo hàm của hàm số y=(2x+1)ln(1-x) là
Tìm đạo hàm của các hàm số sau:1, y3^{(dfrac{x}{ln(x)})}2, ydfrac{1}{2}tan^2(x)+ln(tan(x))3, ysqrt[3]{ln^2(2x)}
Đọc tiếp
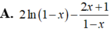
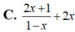
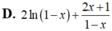
Tìm đạo hàm của các hàm số sau:
1, \(y=3^{(\dfrac{x}{\ln(x)})}\)
2, \(y=\dfrac{1}{2}tan^2(x)+\ln(tan(x))\)
3, 
\(y=\sqrt[3]{ln^2(2x)}\)
1.
\(y'=\left(\dfrac{x}{lnx}\right)'.3^{\dfrac{x}{lnx}}.ln3=\dfrac{lnx-1}{ln^2x}.3^{\dfrac{x}{lnx}}.ln3\)
2.
\(y'=\left(tanx\right)'.tanx+\left(tanx\right)'.\dfrac{1}{tanx}=\dfrac{tanx}{cos^2x}+\dfrac{1}{tanx.cos^2x}\)
3.
\(y=\left(ln2x\right)^{\dfrac{2}{3}}\Rightarrow y'=\left(ln2x\right)'.\dfrac{2}{3}.\left(ln2x\right)^{-\dfrac{1}{3}}=\dfrac{1}{3x\sqrt[3]{ln2x}}\)
Đúng 1
Bình luận (2)
Đạo hàm cấp 5 của hàm số y x ln x là A. B. C. D.
Đọc tiếp
Đạo hàm cấp 5 của hàm số y =x ln x là
A. 
B. 
C. 
D. 
Đạo hàm của hàm số
y
ln
(
x
2
+
1
-
x
)
Đọc tiếp
Đạo hàm của hàm số y = ln ( x 2 + 1 - x )
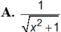
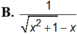
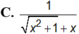
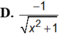
Tính đạo hàm của hàm số :
\(y=\frac{\ln x}{x}+\frac{1+\ln x}{1-\ln x}\)
\(y'=\frac{\frac{1}{x}x-\ln x}{x^2}+\frac{-\frac{1}{x}\left(x+\ln x\right)-\frac{1}{x}\left(x-\ln x\right)}{\left(1+\ln_{ }x\right)^2}=\frac{1-\ln x}{x^2}+\frac{-2}{x\left(1+\ln_{ }x\right)^2}\)
Đúng 0
Bình luận (0)
Tìm đạo hàm của hàm số
y
l
n
(
x
+
x
2
-
1
)
.
A.
y
2
x
x
2
-
1
B.
y
1
x
+...
Đọc tiếp
Tìm đạo hàm của hàm số y = l n ( x + x 2 - 1 ) .
A. y ' = 2 x x 2 - 1
B. y ' = 1 x + x 2 - 1
C. y ' = 1 + x x + x 2 - 1
D. y ' = 1 x 2 - 1
Tìm đạo hàm của hàm số
y
ln
(
x
2
+
x
+
1
)
Đọc tiếp
Tìm đạo hàm của hàm số y = ln ( x 2 + x + 1 )
