Tập nghiệm của phương trình 9 x + 1 = 27 2 x + 1 là
![]()
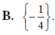
![]()
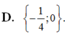
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Tìm tập nghiệm của bất phương trình: 2 x 2 < 2 7 - x
A. x < 3 B. x ≥ 1
C. 1 ≤ x < 3 D. x < 1
Phương trình 2 - f ( x ) = f ( x ) có tập nghiệm T 1 = 20 ; 18 ; 3 . Phương trình 2 g ( x ) - 1 + 3 g ( x ) - 2 3 = 2 g ( x ) có tập nghiệm T 2 = 0 ; 3 ; 15 ; 19 . Hỏi tập nghiệm của phương trình f ( x ) g ( x ) + 1 = f ( x ) + g ( x ) có bao nhiêu phần tử?
A. 4
B. 3
C. 11
D. 6
Đúng ghi Đ, sai ghi S. Điền vào chỗ chấm:
a) Phương trình 2 x + 5 = 11 và phương trình 7 x - 2 = 19 là hai phương trình tương đương. ....
b) Phương trình 3 x - 9 = 0 v à x 2 - 9 = 0 là hai phương trình tương đương. ....
c) Phương trình 0 x + 2 = x + 2 - x có tập nghiệm là S = {2} ....
d) Phương trình ( 2 x - 3 ) ( 3 x + 1 ) = 0 có tập nghiệm là S = 3 / 2 ; - 1 / 3 . . . .
Giải các bất phương trình sau và viết tập nghiệm bằng kí hiệu tập hợp:
a) x + 2 7 − 1 21 > 3 x + 1 3 ; b) 1 + x − 2 3 > 5 − x + 3 ( x − 2 ) 3
Phương trình \(\sqrt{2-f\left(x\right)}=f\left(x\right)\) có tập nghiệm A = {1;2;3}. Phương trình \(\sqrt{2.g\left(x\right)-1}+\sqrt[3]{3.g\left(x\right)-2}=2.g\left(x\right)\) có tập nghiệm là B = {0;3;4;5} . Hỏi tập nghiệm của phương trình \(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)+1=f\left(x\right)+g\left(x\right)\)
có bao nhiêu phần tử?
A.1
B.4 C.6 D.7
\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử
Tập nghiệm của bất phương trình\(\left(x+2\right)\sqrt{x^2-9}\le0\)
x=\(\left\{{}\begin{matrix}x=3\\x=-3\\x=-2\end{matrix}\right.\)
\(\Rightarrow\) (-\(\infty\); -3] \(\cup\) { 3 }
Cho hai phương trình (với cùng ẩn x): \({x^2} - 3x + 2 = 0\,\,\,\left( 1 \right)\)và \(\left( {x - 1} \right)\left( {x - 2} \right) = 0\,\,\,\left( 2 \right)\)
a) Tìm tập nghiệm \({S_1}\) của phương trình (1) và tập nghiệm \({S_2}\) của phương trình (2)
b) Hai tập \({S_1},{S_2}\) có bằng nhau hay không?
a) Phương trình: \({x^2} - 3x + 2 = 0\,\,\,\left( 1 \right)\)
Ta có: \(\Delta = 9 - 4.2 = 1 > 0\)
Phương trình (1) có hai nghiệm \(\left\{ \begin{array}{l}{x_1} = \frac{{3 + 1}}{{2.1}} = 2\\{x_1} = \frac{{3 - 1}}{{2.1}} = 1\end{array} \right.\) => \({S_1} = \left\{ {1;2} \right\}\)
Phương trình: \(\left( {x - 1} \right)\left( {x - 2} \right) = 0\,\,\,\left( 2 \right)\)\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\) => \({S_2} = \left\{ {1;2} \right\}\)
b) Hai tập \({S_1};{S_2}\) có bằng nhau
Tập nghiệm S của bất phương trình tan π 7 x 2 - x - 9 ≤ tan π 7 x - 1
A. S = - 2 2 ; 2 2
B. S = ( - ∞ ; - 2 2 ] ∪ [ 2 2 ; + ∞ )
C. - 2 ; 4
D. S = ( - ∞ ; 2 ] ∪ [ 4 ; + ∞ )
Gọi E là tập nghiệm của phương trình \({x^2} - 2x - 3 = 0\).
G là tập nghiệm của phương trình \((x + 1)(2x - 3) = 0\)
Tìm \(P = E \cap G\).
Ta có:
\({x^2} - 2x - 3 = 0 \Leftrightarrow (x + 1)(x - 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right. \Rightarrow E = \{ - 1;3\} \)
Lại có: \((x + 1)(2x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{3}{2}\end{array} \right.\)
\( \Rightarrow G = \left\{ { - 1;\frac{3}{2}} \right\}\)
\( \Rightarrow P = E \cap G = \left\{ { - 1} \right\}\).
Xét phương trình \(x^2-2x-3=0\) có: \(a-b+c=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=3\end{matrix}\right.\Rightarrow E=\left\{-1;3\right\}.\)
Xét phương trình \(\left(x+1\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\Rightarrow G=\left\{-1;\dfrac{3}{2}\right\}.\)
\(\Rightarrow P=E\cap G=\left\{-1\right\}.\)