Cho hình chóp S.ABCD có đáy ABC vuông tại B, (SAC) vuông góc với (ABC), biết SB = SC = a , SA = BC = a 3 . Gọi α là góc tạo bởi SA và (SBC). Tính sin α
A. sin α = 2 13
B. sin α = 3 13
C. sin α = 1 3 13
D. sin α = 1 2 13
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, cạnh bên SA vuông góc với đáy. Biết BA=a, SC= a căn 3. Góc giữa SB và (SAC)
Xem chi tiết
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)
Đúng 0
Bình luận (0)
a,Tính góc giữa SC và ( ABC) b, Tính góc giữa ( SBC ) Và ( ABC) Biết: 1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA asqrt{3}, SB a
Đọc tiếp
a,Tính góc giữa SC và ( ABC)
b, Tính góc giữa ( SBC ) Và ( ABC)
Biết:
1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ
2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA= \(a\sqrt{3}\), SB= a
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, ABa. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng
45
0
. A.
a
3
3
4
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 45 0 .
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, ABa. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng
45
0
.
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 45 0 .
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại B,
A
B
3
a
,
B
C
4
a
, mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết
S
B
2
3
a
,
S
B
C
^
30
°
. Tính khoảng cách từ B đến mặt phẳng (SAC) . A....
Đọc tiếp
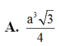
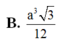
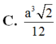
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại B, A B = 3 a , B C = 4 a , mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết S B = 2 3 a , S B C ^ = 30 ° . Tính khoảng cách từ B đến mặt phẳng (SAC) .
A. 6 7 a
B. 6 7 a 7
C. 3 7 14
D. a 7
Đáp án B
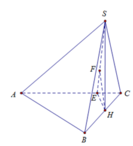
Ta có: A C = 5 a , dựng S H ⊥ B C ⇒ S H ⊥ S B C
Khi đó: S H = S B sin 30 ∘ = a 3 ; H B = S B c os 30 ∘ = 3 a
Suy ra B C = 4 H C ⇒ d B ; S A C = d H ; S A C
d B ; A C = 4 d H ; A C ⇒ d H ; A C = H E = 3 a 5 .
Khi đó H F = S H . H E S H 2 + H E 2 = 3 a 7 14 ⇒ d B = 6 a 7 7 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).
Cho hình chóp S.ABC có (SAB),(SAC) cùng vuông góc với mặt phẳng đáy, cạnh bên SB tạo với đáy một góc 60° đáy ABC là tam giác vuông cân tại B với BA BC a. Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện A.BMNC A.
a
3
3
4
B.
a
3...
Đọc tiếp
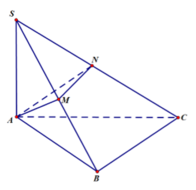
Cho hình chóp S.ABC có (SAB),(SAC) cùng vuông góc với mặt phẳng đáy, cạnh bên SB tạo với đáy một góc 60° đáy ABC là tam giác vuông cân tại B với BA = BC = a. Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện A.BMNC
A. a 3 3 4
B. a 3 3 6
C. a 3 3 24
D. a 3 3 8
Cho hình chóp S.ABC có SA vuông góc với đáy, SA=2a, SA vuông góc với đáy, gọi H, K lần lượt là hình chiếu vuông góc của A trên SB, SC; biết tam giác ABC đều cạnh a. Xác định góc giữa các mặt phẳng : (SBC) và (SAC)
Cho hình chóp S.ABCD , tam giác ABC vuông góc tại C , SA vuông góc với (ABC ) a. CMR : BC vuông góc (SAC) b. Gọi E là hình chiếu của A lê SC . CMR : AE vuông góc ( SBC )
Chắc là chóp SABC vì điểm D không thấy liên quan gì (có hay không cũng không ảnh hưởng bài toán)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
b.
Do \(E\in SC\Rightarrow AE\in\left(SAC\right)\)
Mà \(BC\Rightarrow\left(SAC\right)\Rightarrow BC\perp AE\)
Lại có \(AE\perp SC\left(gt\right)\)
\(\Rightarrow AE\perp\left(SBC\right)\)
Đúng 2
Bình luận (1)