Cho hàm số y = - x 3 + 3 x 2 - 5 . Các mệnh để sau mệnh đề nào sai.
A. Hàm số đồng biến ( 0; 2)
B. Hàm số nghịch biến trên 3 ; + ∞
C. Hàm số nghịch biến trên khoảng - ∞ ; 0
D. Hàm đạt cực đại tại x = 0, y = -5
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây
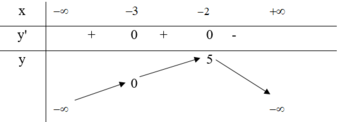
I. Hàm số đồng biến trên khoảng - 3 ; - 2
II. Hàm số đồng biến trên khoảng - ∞ ; 5
III. Hàm số nghịch biến trên các khoản - 2 ; + ∞
IV. Hàm số đồng biến trên khoảng - ∞ ; - 2
Số mệnh đề sai trong các mệnh đề trên là
A. 2
B. 3
C. 4
D. 1
Đáp án D
Khẳng định số II sai.
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng - ∞ ; - 2
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây.
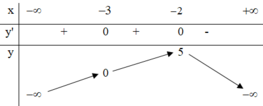
I. Hàm số đồng biến trên khoảng (-3;-2)
II. Hàm số đồng biến trên khoảng − ∞ ; 5 .
III. Hàm số nghịch biến trên các khoản − 2 ; + ∞ .
IV. Hàm số đồng biến trên khoảng − ∞ ; − 2 .
Số mệnh đề sai trong các mệnh đề trên là
A. 2
B. 3
C. 4
D. 1
Đáp án D
Khẳng định số II sai. Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( − ∞ ; − 2 )
Câu 4. Cho hàm số \(y = x^4 - 2x^2 -3\). Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số nghịch biến trên \((-1; 0).\)
B. Hàm số đồng biến trên \((-\infty;0).\)
C. Hàm số nghịch biến trên \((-1; 1).\)
D. Hàm số nghịch biến trên \((0; +\infty).\)
\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây.
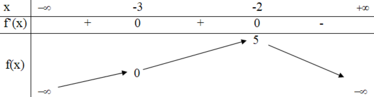
I. Hàm số đồng biến trên khoảng (-3;-2)
II. Hàm số đồng biến trên khoảng − ∞ ; 5 .
III. Hàm số nghịch biến trên khoảng − 2 ; + ∞ .
IV. Hàm số đồng biến trên khoảng - ∞ ; - 2
Số mệnh đề sai trong các mệnh đề trên là
A. 2.
B. 3.
C. 4.
D. 1.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y = x + 1 1 - x và các mệnh đề sau
(1) Hàm số trên nhận điểm I(1;-1) làm tâm đối xứng,
(2) Hàm số trên nhận đường thẳng y = -x làm trục đối xứng.
(3) Hàm số trên nhận y = -1 là tiệm cận đứng.
(4) Hàm số trên luôn đồng biến trên R.
Trong số các mệnh đề trên, số mệnh đề sai là
A. 1
B. 2
C. 3
D. 4
Chọn B
+ Hàm số có tiệm cận đứng x=1 và tiệm cận ngang y= -1. Giao điểm của hai đường tiệm cận là I(1; -1) là tâm đối xứng của đồ thị. Mệnh đề 1 đúng, mệnh đề 3 sai.
+ Vì đường thẳng y=-x là một phân giác của góc tạo bởi 2 đường tiệm cận nên đường thẳng y=-x là một trục đối xứng của đồ thị hàm số. Mệnh đề 2 đúng.
+ Hàm số có tập xác định là R\{1}, nên hàm số không thể luôn đồng biến trên R.Mệnh đề 4 sai.
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 và các mệnh đề sau:
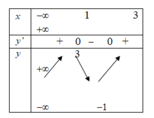
(1) Hàm số đồng biến trên các khoảng − ∞ ; 1 và 3 ; + ∞
nghịch biến trên khoảng (1;3)
(2) Hàm số đạt cực đại tại x = 3và x = 1
(3) Hàm số có y C D + 3 y C T = 0
(4) Hàm số có bảng biến thiên và đồ thị như hình vẽ.
Tìm số mệnh đề đúng trong các mệnh đề trên.
A. 1
B. 4
C. 2
D. 3
Đáp án D
Phương pháp: +) Khảo sát sự biến thiên của đồ thị hàm số.
+) Hàm số đạt cực trị tại điểm x = x 0 ⇔ y ' x 0 = 0 và x = x 0 được gọi là điểm cực trị.
+) Hàm số đạt cực trị tại điểm x = x 0 thì y x 0 là giá trị cực trị.

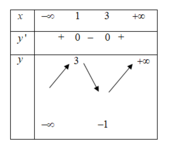

Như vậy có 3 mệnh đề đúng.
Chú ý: Học sinh thường giá trị cực trị và
điểm cực trị nên có thể chọn sai mệnh dề (2) đúng.
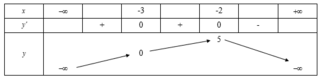
Cho hàm số y = f x liên tục trên R và có bảng biến thiên như hình dưới đây. Bao nhiêu mệnh đề sai trong các mệnh đề sau đây?
I. Hàm số đồng biến trên các khoảng - ∞ ; - 5 và ( - 3 ; - 2 ] .
II. Hàm số đồng biến trên khoảng - ∞ ; 5 .
III. Hàm số nghịch biến trên khoảng - 2 ; + ∞ .
IV. Hàm số đồng biến trên khoảng ( - ∞ ; - 2 ] .
A. 1
B. 2
C. 3
D. 4
Cho hàm số y = f (x) có đạo hàm trên khoảng I. Xét các mệnh đề sau
(I). Nếu f’(x) ≥ 0, ∀ x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số f đồng biến trên I.
(II). Nếu f’(x) ≤ 0, ∀ x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số f nghịch biến trên I.
(III). Nếu f’(x) ≤ 0, ∀ x ∈ I thì hàm số f nghịch biến trên khoảng I.
(IV). Nếu f’(x) ≤ 0, ∀ x ∈ I và f’(x) = 0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I.
Trong các mệnh đề trên, mệnh đề nào đúng, mệnh đề nào sai?
A. I và II đúng, còn III và IV sai
B. I, II và III đúng, còn IV sai
C. I, II và IV đúng, còn III sai
D. Cả I, II, III và IV đúng