Cho x>0 va x2 + 1/(x2) = 7. tính : x8 + 1/(x8)

Những câu hỏi liên quan
Cho x1 + x2 + x3 +...+ x49 + x50 + x51=0 và x1 + x2 = x3 +x4 =x5 + x6= x7 +x8=.....=x49 + x50= x50+ x51= 1. Tính x50
Cho x1 + x2 + x3 +...+ x49 + x50 + x51=0 và x1 + x2 = x3 +x4 =x5 + x6= x7 +x8=.....=x49 + x50= x50+ x51= 1. Tính x51
Ta có : x1 + x2 + ... + x49 + x50 + x51 = 0
x1 + x2 = x3 + x4 = x5 + x6 = x7 + x8 = ... = x49 + x50 = x50 + x51 = 1
\(\Rightarrow\)x1 + x2 + ... + x49 + 2x50 + x51 = 1 + 1 + ... + 1 + 1 = 26
\(\Rightarrow\)x50 = 26
Từ đó suy ra : x51 = 1 - 26 = -25
Đúng 0
Bình luận (0)
D = ( x2 + x + 1)( x21 -x+1)( x4 - x2 + 1)( x8 - x4 + 1)
Bạn cần viết đầy đủ đề: Bao gồm yêu cầu đề và công thức toán để được hỗ trợ tốt hơn.
Đúng 0
Bình luận (0)
\(D=\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left[\left(x^2+1\right)^2-x^2\right]\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left(x^4+x^2+1\right)\left(x^4-x^2+1\right)\cdot\left(x^8-x^4+1\right)\)
\(=\left(x^8+2x^4+1-x^4\right)\left(x^8-x^4+1\right)\)
\(=\left(x^8+1\right)^2-x^8\)
\(=x^{16}+x^8+1\)
Đúng 0
Bình luận (0)
Anh chị giúp em giải bài toán này được không ạ?
Tìm x1,x2,...,x9, biết:
x1+1/9 = x2+2/8 = x3+3/7 = ... =x8+8/2 = x9+9/1 và x1+x2+x3+...+x8+x9=90
Ta có \(x1-\frac{1}{9}=x2-\frac{2}{8}=...=x9-\frac{9}{1}\)
\(=\frac{x1-1}{9}=\frac{x2-2}{8}=\frac{x3-3}{7}=...=\frac{x9-9}{1}\)
= \(\frac{x1-1+x2-2+x3-3+...+x9-9}{9+8+7+...+1}\)
\(=\frac{\left(x1+x2+x3+...+x9\right)-\left(1+2+3+...+9\right)}{9+8+7+....+1}\)
=\(\frac{90-45}{45}=\frac{45}{45}=1\)
=> \(\hept{\begin{cases}\begin{cases}x1=10\\x2=10\end{cases}\\.....\\x9=10\end{cases}}\)
Đúng 1
Bình luận (0)
Tìm x
a,(x+2)2-2x(2x+3)=(x+1)2
b,6x3+x2=2x
c,x8-x5+x2-x+1=0
Bn viết kiểu gì vậy,6x3 là 18x hay là 6x\(^3\)
Đúng 0
Bình luận (0)
Tính giá trị của các đa thức sau: x2 + x4 + x6 + x8 + … + x100 tại x = -1
Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 = 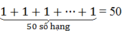
Vậy giá trị đa thức bằng 50 tại x = -1.
Đúng 0
Bình luận (0)
Với x ≠ 0 ta có x 8 : x 2 bằng
A. x 4
B. x 6
C. x x
D. x 10
Tìm các số x1,x2,x3,...,x8,x9 biết \(\frac{x1+1}{9}=\frac{x2+2}{8}=\frac{x3+3}{7}=...=\frac{x8+8}{2}=\frac{x9+9}{1}\)
Thực hiện các phép tính sau:a)
y
4
x
2
−
2
xy
+
4
x
2
y
2
−
4
xy
với
x
≠
0
và
y
≠...
Đọc tiếp
Thực hiện các phép tính sau:
a) y 4 x 2 − 2 xy + 4 x 2 y 2 − 4 xy với x ≠ 0 và y ≠ 2 x ;
b) 1 1 − x + 1 1 + x + 2 1 + x 2 + 4 1 + x 4 + 8 1 + x 8 + 16 1 + x 16 với x ≠ ± 1 .
rút gọn đa thức:
a(x+1)(x-1)
b(x+1)(x-1)(x2+1)
c(x+1)(x-1)(x2+1)(x4+1)-x8
a) \(\left(x+1\right)\left(x-1\right)\)
\(=x^2-1^2\)
\(=x^2-1\)
b) \(\left(x+1\right)\left(x-1\right)\left(x^2+1\right)\)
\(=\left(x^2-1\right)\left(x^2+1\right)\)
\(=\left(x^2\right)^2-1^2\)
\(=x^4-1\)
c) \(\left(x+1\right)\left(x-1\right)\left(x^2+1\right)\left(x^2+1\right)-x^8\)
\(=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)-x^8\)
\(=\left(x^4-1\right)\left(x^4+1\right)-x^8\)
\(=\left(x^4\right)^2-1-x^8\)
\(=x^8-1-x^8\)
\(=-1\)
Đúng 2
Bình luận (0)




















