Cho tam giác ABC, tia phân giác góc B cắt AC tại E. Tính A E B ^ và B E C ^ biết 2 C ^ + B ^ = 150 ° .

Những câu hỏi liên quan
Cho tam giác ABC có A= 180 độ - 3C và B=70 độ
a) Tính số đo góc A và C của tam giác ABC;
b) Vẽ tia phân giác của góc B cắt AC tại E. Qua E kẻ đường thẳng song song với BC cắt AB tại D.
\(a,\widehat{A}+\widehat{B}+\widehat{C}=180\\ \Rightarrow180-3\widehat{C}+\widehat{C}+70=180\\ \Rightarrow-2\widehat{C}=-70\\ \Rightarrow\widehat{C}=35\\ \Rightarrow\widehat{A}=180-35=145\)
Đúng 3
Bình luận (0)
Cho tam giác ABC, tia phân giác góc A cắt BC tại D và tia phân giác góc B cắt AC tại E, biết góc BEC = góc ADB. Tính góc C
Cho tam giác ABC, tia phân giác góc A cắt BC tại D và tia phân giác góc B cắt AC tại E, biết góc BEC = góc ADB. Tính góc C
Cho tam giác ABC biết góc nhọn tạo bởi 2 tia phân giác góc B, góc C bằng 60 độ.
a) Tính góc A của tam giác ABC
b) Tia phân giác góc B cắt AC tại D và tia phân giác góc C cắt AB tại E. CMR: góc BEC và góc BDC bù nhau
Cho tam giác ABC, tia phân giác góc A cắt BC tại D và tia phân giác góc B cắt AC tại E, biết góc BEC bằng góc ADB. Tính góc C
Cho tam giác ABC vuông ở A. Tia phân giác của góc B cắt AC tại E
C
^
-
B
^
26
o
. Tính
A
B
E
^
và
B
E
C
^
A. ...
Đọc tiếp
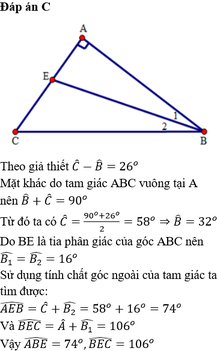
Cho tam giác ABC vuông ở A. Tia phân giác của góc B cắt AC tại E
C ^ - B ^ = 26 o . Tính A B E ^ và B E C ^
A. A B E ^ = 70 ° , B E C ^ = 110 °
B. A B E ^ = 106 ° , B E C ^ = 74 °
C. A B E ^ = 74 ° , B E C ^ = 106 °
D. A B E ^ = 60 ° , B E C ^ = 120 °
1, Cho tam giác ABC và ADE có góc đỉnh A là hai góc đối đỉnh , trong đó 3 điểm B,A,E thẳng hàng . Phân giác trong của góc C và E cắt nhau tại F . Tính góc EFC theo góc B và D2, Cho tam giác ABC biết rằng góc nhọn tạo bởi tia phân giác của góc B và C có số đo bằng 60 độ . Tính a, Góc A b, Tia phân giác góc B cắt AC ở D . Tia phân giác góc C cắt AB ở E . Chứng minh rằng hai góc BEC và BDC bù nhau
Đọc tiếp
1, Cho tam giác ABC và ADE có góc đỉnh A là hai góc đối đỉnh , trong đó 3 điểm B,A,E thẳng hàng . Phân giác trong của góc C và E cắt nhau tại F . Tính góc EFC theo góc B và D
2, Cho tam giác ABC biết rằng góc nhọn tạo bởi tia phân giác của góc B và C có số đo bằng 60 độ . Tính
a, Góc A
b, Tia phân giác góc B cắt AC ở D . Tia phân giác góc C cắt AB ở E . Chứng minh rằng hai góc BEC và BDC bù nhau
Bài 1. Cho tam giác ABC có A= 80◦ và 2B = 3C. a) Tính các góc B và C. b) Tia phân giác của góc B cắt AC tại D. Đường thẳng qua A song song với BD cắt tia CB tại E. Chứng minh rằng tam giác ABE cân. c) Tia phân giác của góc ABE cắt AE tại F. Chứng minh rằng BF là đường trung trực của AE.
a: \(\widehat{B}=60^0;\widehat{C}=40^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB<AC) . 2 tia pân giác trong của góc B,C cắt nhau tại I. 2 tia phân giác ngoài tại B và C cắt nhau ở E .
Chứng minh A,I,E
IB,BE là hai tia phân giác của hai góc kề bù
=>BI vuông góc BE
CI,CE là hai tia phân giác của hai góc kề bù
=>CI vuông góc CE
góc IBE+góc ICE=90+90=180 độ
=>BICE nội tiếp
=>góc BIE=góc BCE
góc IAB+góc IAB=(góc BAC+góc CBA)/2=(180 độ-góc ACB)/2=90 độ-1/2*góc ACB
=>góc AIB=180 độ-90 độ+1/2*góc ACB
=90 độ+1/2*góc ACB
góc AIB+góc BIE
=90 độ+1/2*góc ACB+90 độ-1/2*góc ACB
=180 độ
=>A,I,E thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC, A=70o, C=30o. Tia phân giác của góc B cắt AC tại D
a. Tính góc ABC và góc ACB
b. Tia phân giác của góc C cắt AB ở E và cắt BD ở I. Tính góc BIC và góc CID