Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M di động trên cạnh SC, đặt M C M S . Mặt phẳng qua A, M song song với BD cắt SB, SD thứ tự tại N, P. Thể tích khối chóp C.APMN lớn nhất khi
A. k= 3
B. k=1
C. k=2
D. k= 2
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M di động trên cạnh SC, đặt M C M S = k . Mặt phẳng qua A, M song song với BD cắt SB, SD thứ tự tại N, P. Thể tích khối chóp C.APMN lớn nhất khi
A. k = 3 .
B. k=1
C. k=2
D. k = 2 .
Đáp án D
Phương pháp giải:
Dùng định lí Thalet, định lý Menelaus và phương pháp tỉ số thể tích để tính thể tích khối chóp theo tham số k.
Khảo sát hàm số chứa biến k để tìm giá trị lớn nhất – giá trị nhỏ nhất
Lời giải:
Gọi O là tâm của hình bình hành ABCD và I = S O ∩ A M .
Ba điểm M,A,I thẳng hàng nên áp dụng định lý Menelaus cho tam giác SOC ta có: S M M C . C A A O . O I I S = 1 ⇒ O I S I = 1 = k 2 .
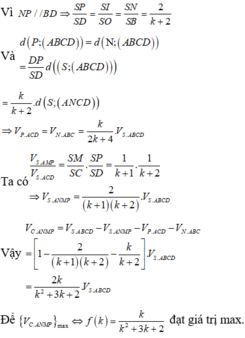

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, tam giác SBD đều cạnh a. Gọi M, P là hai điểm lần lượt di động trên cạnh SA, SC (không trùng với S) sao cho SA/SM + SC/ SP = 3, (a) là mặt phẳng di động chứa M, P cắt SB, SD lần lượt tại N, Q. Diện tích tam giác SNQ đạt giá trị nhỏ nhất là
Bài này ứng dụng 1 phần cách giải của bài này:
Gọi O' là giao điểm của SO và MP, tương tự như bài trên, ta có 3 đường thẳng SO, MP, NQ đồng quy tại O'
Đồng thời sử dụng diện tích tam giác, ta cũng chứng minh được:
\(3=\dfrac{SA}{SM}+\dfrac{SC}{SP}=\dfrac{2SO}{SO'}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\)
Áp dụng BĐT Cô-si: \(3=\dfrac{SB}{SN}+\dfrac{SD}{SQ}\ge2\sqrt{\dfrac{SB.SD}{SN.SQ}}\Rightarrow SN.SQ\ge\dfrac{4}{9}.SB.SD\)
Theo bổ đề về diện tích tam giác chứng minh ở đầu:
\(\dfrac{S_{SNQ}}{S_{SBD}}=\dfrac{SN.SQ}{SB.SD}\ge\dfrac{\dfrac{4}{9}SB.SD}{SB.SD}=\dfrac{4}{9}\)
\(\Rightarrow S_{SBD}\ge\dfrac{4}{9}.S_{SBD}=\dfrac{4}{9}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{9}\)
Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi C' là trung điểm của SC và M là một điểm di động trên cạnh SA. Mặt phẳng (P) di động luôn đi qua C'M và song song với BC.
a) Xác định thiết diện (P) cắt hình chóp S.ABCD. Xác định vị trí điểm M để thiết diện là hình bình hành.
b) Khi M di động trên cạnh SA, thì giao điểm của hai cạnh đối của thiết diện chạy trên đường nào?
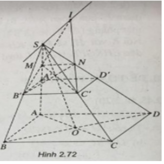
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B'C' song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A' của cạnh SA thì thiết diện MB'C'N' là hình bình hành.
b) Với M không trùng với A':
Gọi I ∈ B′M ∩ C′N. Ta có:
I ∈ B′M ⊂ (SAB), tương tự I′ ∈ C′N ⊂ (SCD)
Như vậy I ∈ Δ = (SAB) ∩ (SCD).
Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi C' là trung điểm của SC và M là một điểm di động trên cạnh SAa. Mặt phẳng (P) di động luôn đi qua C'M và song song với BC
a) Xác định thiết diện (P) cắt hình chóp S.ABCD. Xác định vị trí điểm M để thiết diện là hình bình hành
b) Khi M di động trên cạnh SA, thì giao điểm của hai cạnh đối của thiết diện chạy trên đường nào ?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và một điểm \(M\) di động trên cạnh \(AD\). Một mặt phẳng \(\left( \alpha \right)\) qua \(M\), song song với \(C{\rm{D}}\) và \(SA\), cắt \(BC,SC,SD\) lần lượt tại \(N,P,Q\).
a) \(MNPQ\) là hình gì?
b) Gọi \(I = MQ \cap NP\). Chứng minh rằng \(I\) luôn luôn thuộc một đường thẳng cố định khi \(M\) di động trên \(AD\).
Tham khảo hình vẽ:
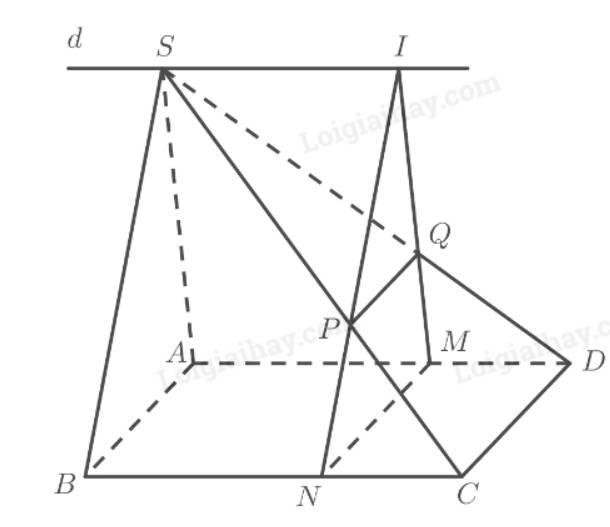
a) Ta có:
\(\begin{array}{l}MN = \left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {SC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\PQ = \left( \alpha \right) \cap \left( {SC{\rm{D}}} \right)\\MN\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(MN\parallel C{\rm{D}}\parallel PQ\).
\( \Rightarrow MNPQ\) là hình bình hành.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in MQ \Rightarrow I \in \left( {SA{\rm{D}}} \right)\\I \in NP \Rightarrow I \in \left( {SBC} \right)\end{array} \right\} \Rightarrow I \in \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\ \Rightarrow SI = \left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\BC\parallel A{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(A{\rm{D}}\parallel BC\parallel SI\).
Vậy \(I\) luôn luôn thuộc đường thẳng \(d\) đi qua \(S\) song song với \(AD\) và \(BC\) cố định khi \(M\) di động trên \(AD\).
Bài 3 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M, N là trung điểm cạnh SC; SD
a) CMR: MN // (SAB); MM // (ABCD)
b) CMR: MO // (SAB)
Bài 4 :Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M,N, P là trung điểm cạnh SA, SB, SC.
a) Chứng minh rằng : MN // (SCD).
b) Chứng minh rằng: MO // (SAB)
Giúp vs bạn !!
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là điểm di động trên cạnh SC (M không trùng S và C), mặt phẳng α chứa đường thẳng AM song song với BD lần lượt cắt các cạnh SB, SD tại E và F. Giá trị T = S B S E + S D S F - S C S M bằng
![]()
![]()
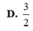
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là điểm di động trên cạnh SC (M không trùng S và C), mặt phẳng (α) chứa đường thẳng AM song song với BD lần lượt cắt các cạnh SB, SD tại E và F. Giá trị T = S B S E + S D S F - S C S M bằng
A. 1
B. 2
C. 1 2
D. 3 2
Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, cho điểm M thay đổi trên cạnh SD
Xác định giao điểm N của SC và mặt phẳng (ABM). Tứ giác ABNM là hình gì ? Có thể là hình bình hành không ?
Hai mặt phẳng (MAB) và (SCD) có điểm chung M và lần lượt chứa hai đường thẳng song song AB và CD nên giao tuyến của chúng là đường thẳng d' đi qua M và song song với AB và CD. Vậy qua M ta sẽ vẽ đường thẳng d', đường thửng này cắt SC tại N. Đây là điểm cần tìm. Ta thấy ngay ABNM là hình thang. Để ABNM là hình bình hành, ta phải có thêm AM song song với BN. Khi đó AM và BN phải song song với d. Điều này không thể xảy ra khi M thuộc đoạn SD và không trùng với hai đầu mút S và D