Phát biểu các tính chất của hình bình hành, hình chữ nhật, hình thoi, hình vuông.

Những câu hỏi liên quan
Phát biểu các tính chất của hình bình hành, hình chữ nhật, hình thoi, hình vuông ?
- Hình chữ nhật có tính chất :
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường + Tất cả các tính chất của hình thang cân và hình thoi. - Hình thoi có tính chất : + Hai đường chéo vuông góc với nhau + Hai đường chéo là các đường phân giác của các góc của hình thoi và cắt nhau tại trung điểm của mỗi đường + Tất cả các tính chất của hình bình hành- Hình bình hành có tính chất:
+ Các cạnh đối bằng nhau + Các góc đối bằng nhau + Hai đường chéo cắt nhau tại trung điểm của mỗi đường Hình vuông có tính chất : - Hình vuông có các tính chất của hình chữ nhật và hình thoi.
Đúng 0
Bình luận (0)
| hình bình hành |
- các cạnh đối bằng nhau |
| hình chữ nhật |
- Cạnh: 2 cạnh đối song song và bằng nhau |
| hình thoi | - Cạnh: cạnh đối song song, 4 cạnh bằng nhau - Góc: góc đối bằng nhau - Đường chéo: 2 đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường |
| hình vuông |
- Cạnh: 4 cạnh bằng nhau, cạnh đối song song |
Đúng 1
Bình luận (0)
Phát biểu định nghĩa hình bình hành, hình chữ nhật, hình thoi, hình vuông.
- Hình bình hành là tứ giác có các cạnh đối song song.
- Hình chữ nhật là tứ giác có bốn góc vuông.
- Hình thoi là tứ giác có bốn cạnh bằng nhau.
- Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Đúng 0
Bình luận (0)
Phát biểu định nghĩa hình bình hành, hình chữ nhật, hình thoi, hình vuông ?
_ Hình bình hành là tứ giác có các cạnh đối song song.
_ Hình chữ nhật là tứ giác có bốn góc vuông.
_ Hình thoi là tứ giác có bốn cạnh bằng nhau.
_ Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Các hình 2.70a, 2.70b, 2.70c, 2.70d là hình biểu diễn của các hình bình hành nào (hình bình hành, hình thoi, hình vuông, hình chữ nhật)?
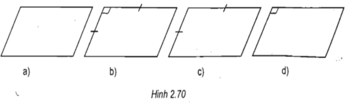
Hình 2.70a biểu diễn hình bình hành
Hình 2.70b biểu diễn hình vuông
Hình 2.70c biểu diễn hình thoi
Hình 2.70d biểu diễn hình chữ nhật
Đúng 0
Bình luận (0)
Câu 24: Phát biểu nào sai
A.Hình bình hành có một góc vuông là hình chữ nhật
B.Hình chữ nhật có hai cạnh liên tiếp bằng nhau là hình vuông
C.Hình bình hành có hai đường chéo bằng nhau là hình thoi
D.Hình thoi có một góc vuông là hình vuông
Xem thêm câu trả lời
bạn nào bít chỉ với , cần gấp:
chứng minh rằng các trung điểm của bốn cạnh hình chữ nhật là các đỉnh của hình thoi. là theo tính chất hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.
Đúng 0
Bình luận (0)
Cách của tớ giống việt anh
a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.
Đúng 0
Bình luận (0)
=))))))))))))))
Vẽ sơ đồ tư duy tổng hợp kiến thức về:
-Định nghĩa
-Tính chất
-Dấu hiệu nhận biết
Của các tứ giác sau:
-Hình bình hành
-Hình chữ nhật
-Hình thoi
-Hình vuông.
Điền Đ (đúng) hoặc S (sai) trong các phát biểu sau:1. Độ dài đường trung bình của hình thang bằng nửa tổng độ dài hai cạnh hình thang.2. Hình bình hành có hai góc kề một cạnh bằng nhau là hình chữ nhật.3. Hình thoi có 2 đường chéo vuông góc với nhau là hình vuông.4. Hai đường chéo của hình vuông là trục đối xứng của hình vuông.
Đọc tiếp
Điền Đ (đúng) hoặc S (sai) trong các phát biểu sau:
1. Độ dài đường trung bình của hình thang bằng nửa tổng độ dài hai cạnh hình thang.
2. Hình bình hành có hai góc kề một cạnh bằng nhau là hình chữ nhật.
3. Hình thoi có 2 đường chéo vuông góc với nhau là hình vuông.
4. Hai đường chéo của hình vuông là trục đối xứng của hình vuông.
Sơ đồ ở hình 109 biểu thị quan hệ giữa các tập hợp hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Dựa vào sơ đồ đó, hãy điền vào chỗ trống: a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình ... b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình ... c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình ...
Đọc tiếp
Sơ đồ ở hình 109 biểu thị quan hệ giữa các tập hợp hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Dựa vào sơ đồ đó, hãy điền vào chỗ trống:
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình ...
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình ...
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình ...
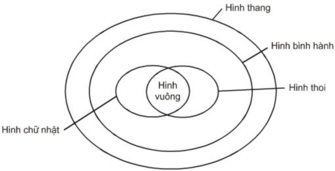
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình bình hành, hình thang.
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình bình hành, hình thang.
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông.
Đúng 0
Bình luận (0)






















