Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung tròn như hình 20.
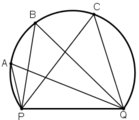
Hãy so sánh các góc PAQ ; PBQ ; PCQ
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung tròn như hình 20.
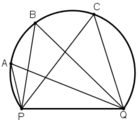
Hãy so sánh các góc P A Q ^ ; P B Q ^ ; P C D ^
Các điểm A, B, C, Q, P cùng thuộc một đường tròn.
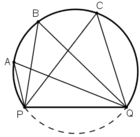
Các góc 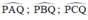 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 
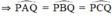
Trong trận đấu bóng đá giữa 2 đội Real madrid và Barcelona, trọng tài cho đội Barcelona được hưởng một quả Penalty. Cầu thủ sút phạt sút ngẫu nhiên vào 1 trong bốn vị trí 1, 2, 3, 4 và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1, 2, 3, 4 với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 (hoặc 2) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 (hoặc 4) thì xác suất cản phá thành công là 50%. Tính xác suất của biến cố “cú sút đó không vào lưới”?

A. 5 16
B. 3 16
C. 1 8
D. 1 4
Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P A = 1 8 + 1 16 = 3 16 .
Trong trận đấu bóng đá giữa 2 đội Real madrid và Barcelona, trọng tài cho đội Barcelona được hưởng một quả Penalty. Cầu thủ sút phạt sút ngẫu nhiên vào 1 trong bốn vị trí 1, 2, 3, 4 và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1, 2, 3, 4 với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 (hoặc 2) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 (hoặc 4) thì xác suất cản phá thành công là 50%. Tính xác suất của biến cố “cú sút đó không vào lưới”?

A. 5 16
B. 3 16
C. 1 8
D. 1 4
Đáp án B
Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 = 1 8 . Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng 2 . 1 4 . 1 4 . 1 2 = 1 16 . Suy ra xác suất để bóng không vào bằng P ( A ) = 1 8 + 1 16 = 3 16 .
Một cầu thủ đang đứng ở vị trí A để sút bóng vào khung thành BC. Tính đường kính của đường tròn đi qua ba điểm A,B,C. Biết góc sút BAC là 68° và chiều rộng của BC là 5m
Trong trận bóng đá, trái bóng đang ở vị trí D, ba cầu thủ đứng thẳng hàng tại vị trí A, B, C trên sân với số áo lần lượt là 4, 2, 3 như Hình 9.1. Theo em cầu thủ nào gần trái bóng nhất, cầu thủ nào xa trái bóng nhất? Tại sao?
(Biết rằng góc ACD là góc tù)
Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.
Sau khi kết thúc một trận đấu đầy kịch tính (trận lượt về giữa VIỆT NAM và PHILIPPINES), đội bóng của hàng triệu người yêu mến đã dành chiến thắng thuyết phục 2-1. Một buổi liên hoan nhẹ cho các cầu thủ, ban huấn luyện, quan chức,… được tổ chức nhanh chóng. Để tiện việc ghi hình, phỏng vấn,… Ban tổ chức dự định sắp xếp hai cầu thủ ghi bàn vào trong cùng một bàn tròn có 10 chỗ ngồi (các chỗ ngồi được đánh số thứ tự) và ngồi đối diện nhau (ví dụ như hai cầu thủ ngồi ở vị trí ghế số 5 và ghế số 10). Hỏi rằng có bao nhiêu cách sắp xếp?
A. 10
B. 20
C 9!
D. 10.8!
Gọi tên hai cầu thủ ghi bàn là A và B.
Cứ mỗi vị trí ngồi của A có đúng một cách sắp xếp A-B. Vì A có 10 vị trí ngồi nên có 10 cách sắp xếp. Chọn A.
Chú ý. Đề chỉ quan tâm đến hai cầu thủ ghi bàn và cách xếp hai cầu thủ này ngồi đối diện trong bàn tròn có 10 chỗ ngồi.
Trong trận đấu bóng đá giữa 2 đội Real Madrid và Barcelona, trọng tài cho đội Barcelona được hưởng 1 quả Penalty. Cầu thủ sút phạt ngẫu nhiên vào trong 4 vị trí 1,2,3,4 sao cho vị trí 1 ở góc dưới bên trái, vị trí 2 ở góc dưới bên phải, vị trí 4 trên vị trí 1 và vị trí 3 trên vị trí 2 (thủ môn và cầu thủ sút phạt ko có khả năng "đọc tâm thuật"). Biết nếu cầu thủ sút và thủ môn bay cùng vô vị trí 1 (hoặc 2) thì thủ môn cản phá được cú sút đó, nếu vô vị trí 3 (hoặc 4) thì xác xuất thành công là 50%. Tính xác suất của biến cố "cú sút đó ko vô lưới"
Những trận đấu giữa Real Madrid và Barcelona luôn rất rất căng thẳng và đỉnh điểm chính là trong giai đoạn 1953-1966 và 2010-2013
Câu hỏi: có 1 đội bóng có 11 cầu thủ.Huấn luyện viên bố chí như sau:
-Cầu thủ số 1 ở bên cánh trái
-Cầu thủ số 2 ở bên cánh phải
Cầu thủ số 3 làm hậu vệ
Cầu thủ số 4 là thủ môn
Cầu thủ số 5 cũng là hậu vệ
Cầu thủ số 6 ở góc cuối phải
Cầu thủ số 7 ở góc cuối trái
Vậy là ông huấn luyện viên đã cho từng cầu thủ mỗi người một chỗ nhưng vẫn thừa 4 người.
Hỏi ông ta phải làm thế nào để cả 11 cầu thủ mỗi người đều có 1 chức vụ (Biết hậu vệ cần 3 người,giũa sân ít nhất là 1 người)
Giúp mình nha
Trong trận đấu bóng đã giữa 2 đội Real malrid và Barcelona , trọng tài cho đội Barcelona hưởng một quả Penalty . Cầu thủ sút phạt ngẫu nhiên vào 1 trong bốn vị trí 1,2,3,4 và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1,2,3,4 với xác xuất như nhau ( thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương ) . Biết cầu thủ sút phạt và thủ môn bay cùng vào vị trí 1 ( hoặc 2) thì thủ môn cản phá được cú sút đó , nếu cùng vào vị trí 3 (hoặc 4 ) thì xác xuất phá thành công là 50% . Tính xác xuất của biến cố " cú sút đó không vào lưới "
Gọi \(A_i\) là biến cố cầu thủ sút vào vị trí \(i\) và \(B_i\) là biến cố thủ môn bay người tới vị trí \(i\)
Do 4 vị trí như nhau nên \(P\left(A_i\right)=P\left(B_i\right)=\dfrac{1}{4}\) với mọi i từ 1 tới 4
Xác suất cầu thủ ko sút vào là:
\(P=P\left(A_1\right).P\left(B_1\right)+P\left(A_2\right).P\left(B_2\right)+\dfrac{1}{2}P\left(A_3\right).P\left(B_3\right)+\dfrac{1}{2}P\left(A_4\right).P\left(B_4\right)\)
\(=\dfrac{1}{4}.\dfrac{1}{4}+\dfrac{1}{4}.\dfrac{1}{4}+\dfrac{1}{2}.\dfrac{1}{4}.\dfrac{1}{4}+\dfrac{1}{2}\dfrac{1}{4}.\dfrac{1}{4}=\dfrac{3}{16}\)