Cho tứ diện ABCD có tam giác ABC là tam giác cân với B A C ⏜ = 120 0 , A B = A C = a . Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16 .
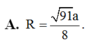
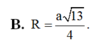
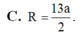
![]()
bài 1 cho tam giác ABC có BC=20cm và diện tích bằng 120
a, tính chiều cao AH của TAM giác ABC
b, gọi M , N lần lượt là trung điểm AB và AC . Tứ giác BMNC là hình gì ? Tính điện tích của tứ giác đó
bài 2 Cho hình thang cân ABCD ( AB//DC) có AC vuông góc BD tại O và AB=4, CD=8
a, Cm cá tam giác OCD và tam giác OAB vuông cân
b , tính Shình thang cân ABCD
Giúp mình với tối mai đi hoc rồi
Gọi chiều cao AH là x :
Áp dụng công thức tính diện tích tam giác ta được :
\(\frac{1}{2}\).BC.AH = 120
\(\frac{1}{2}\).20.x =120
10x =120
x = 12
=) AH = 12 cm
b) Xét tam giác ABC có :
M là trung điểm của AB
N là trung điểm của AC
=) MN là đường trung bình của tam giác ABC
=) MN // BC ; MN=\(\frac{1}{2}\)BC
Xét tứ giác BMNC có
MN // BC
=) Tứ giác BMNC là hình thanh
Giả sử MN cắt AH tại K
Xét tam giác ABH có :
M là trung điểm của AB
MK // BH
=) K là trung điểm của AH
Do K là trung điểm của AH
=) AK=KH=\(\frac{AH}{2}\)=\(\frac{12}{2}\)=6
Ta có MN=\(\frac{BC}{2}\)=10
Diện tích hình thang BMNC là
\(\frac{1}{2}\).KH.(MN+BC)= \(\frac{1}{2}\).6.(10+20)
= 90 cm2
Cho tứ diện ABCD có tam giác ABC là tam giác cân với B A C = 120 0 , A B = A C = a . Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16 .
A. R = 91 a 8 .
B. R = a 13 4 .
C. R = 13 a 2 .
D. R = 6 a .
Đáp án A
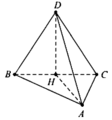
Gọi H là trung điểm của BC, O là tâm đường tròn ngoại tiếp tam giác ABC suy ra H là trung điểm của AO.
Ta có D H = 3. V A B C D S Δ A B C = a 3 4 .
Gọi J là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Khi đó J O ⊥ A B C .
Do J A = R , O A = a nên J O = R 2 − a 2 .
Mặt khác H O ⊥ J O , H O ⊥ H D nên ta có
a 3 4 ± R 2 − a 2 2 + a 2 2 = R 2 ⇔ R = a 91 8 .
Cho tứ diện ABCD có tam giác ABC là tam giác cân với BAC= 120 o ,AB=AC=a Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16

![]()
Cho tứ diện ABCD có ABC là tam giác đều cạnh a tam giác BCD cân tại D và nằm trong mặt phẳng vuông góc với (ABC). Biết AD hợp với mặt phẳng (ABC) một góc 60°. Tính thể tích V của khối tứ diện ABCD.
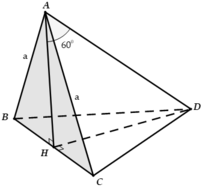
A. V = a 3 3 6
B. V = a 3 12
C. V = a 3 3 8
D. V = a 3 3 24
Cho tứ diện ABCD có tam giác ABC là tam giác cân với góc B A C ⏜ = 120 0 , AB=AC=a. Hình chiếu của D trên mặt phẳng ABC là trung điểm của BC. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD biết thể tích của tứ diện ABCD là V = a 3 16
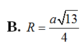
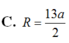
![]()
Câu 1 Cho tứ giác ABCD Gọi Q là trung điểm của AC đường thẳng qua Q cắt AB AC lần lượt tại I và K chứng minh diện tích tam giác AIK bằng diện tích tam giác CIK
Câu 2 Cho tam giác ABC cân tại A Gọi M và N lần lượt là trung điểm của AB và AC .a) chứng minh tứ giác BMNC là hình thang .b). Trên tia đối của tia MN xác định điểm E sao cho NE=NM hỏi tứ giác AECM là hình gì vì sao
Câu 3 Cho tam giác abc vuông tại a gọi D E theo thứ tự là trung điểm của AB BC Tính de biết BC = 10 cm AB = 8 cm
Câu 4 cho tứ giác ABCD có Â = 90° B =60° C =120°. a)tính số đo góc D. b) tứ giác ABCD là hình gì vì sao?
Giúp mình với sắp thi rùi
cho tam giác cân ABC có AM là đường trung tuyến biết AB = 15 cm BC = 18.Gọi D đối xứng với A qua BC. Diện tích tứ giác ABCD là: A: 108cm2 B: 216cm2 C: 270cm2 D: 66cm2
ta có: AB=AC( tam giác ABC cân)
=> tứ giác ABCD là hình thoi
MB=18:2=9 cm
ta có M là trung tuyến cũng là đường cao trong tam giác ABC
áp dụng định lý pitago, ta có:
\(AB^2=BM^2+AM^2\)
\(15^2=9^2+AM^2\)
=>AM=12cm
=>AD= 24cm
=> diện tích tứ giác ABCD là:
\(\dfrac{1}{2}.AD.BC\)
<=>\(\dfrac{1}{2}.24.18=216cm^2\)
Chọn B
Cho tứ diện ABCD có tam giác ABC cân tại \(A\), tam giác BCD cân tại \(D\). Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng \(BC \bot (AID)\).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng \(AH \bot (BCD)\).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.

a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.
Cho tam giác ABC. Phía ngoài tam gíac vẽ các tam giác đều ABD, ACE và tam giác cân BCF có góc F =120°. I đối xứng với F qua BC. K đối xứng với I qua DE.
a) CMR : tam giác DIE cân và góc I = 120 độ
b) tam giác BIK là tam giác gì?
c) Tứ giác AKIF là hình bình hành; AF vuông góc với DE