Cho hình chóp có đáy S . A B C D là hình vuông cạnh a vuông góc với đáy, S A = a . Khoảng cách giữa hai đường thẳng SB và CD là
A. a 3
B. a 2
C. 2 a
D. a
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 2 . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Chọn C
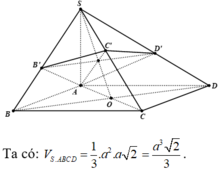
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
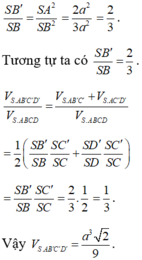

Cho hình chóp S . A B C D có đáy là hình vuông cạnh a . S A = a v à S A vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD
A. d = a 3 2
B. d = a 3 3
C. d = a 6 6
D. d = a 6 3
Đáp án D
Ta có: f ' x = x − 1 x 2 − 2 2 x 2 + 2 đổi dấu khi đi qua điểm x=1 nên hàm số đã cho có duy nhất 1 điểm cực trị.
Đề thiếu dữ liệu để xác định độ dài SA rồi bạn
Cho hình chóp S. ABCD có đáy là hình vuông cạnh a. Biết SA vuông góc với đáy và SA =a.Tính khoảng cách từ điểm A đến mp (SBD)
A. 2 a 3
B. a 3
C. a 2 3
D. a 2 6
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích của khối chóp S. ABCD bằng a 3 3 . Tính khoảng cách từ A đến mặt phẳng (SBE).
A. 2 a 3
B. a 2 3
C. a 3
D. a 3 3
cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy SA=a căn 3 a)cm SAC vuông góc với SBD b)gọi AH là đg cao của tam giác SAB . cmr AK vuông góc với (SBC) c) tính góc giữa đg thẳng SC và mặt đáy ABC d) tính khoảng cách từ a đến mp (SCD)
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy và SA=a, AB=BC=a. Gọi M là điểm thuộc AB sao cho . Tính khoảng cách d từ điểm S đến đường thẳng CM.
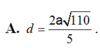
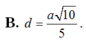
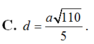
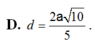
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABD. Cạnh SD tạo với đáy (ABCD) một góc bằng 60 ° . Khoảng cách từ điểm A tới mặt phẳng (SBC) là
A. 2 a 285 57
B. a 285 57
C. a 285 19
D. 2 a 285 19
Cho hình chóp S. ABCD có đáy ABCD là hình vuông tâm O cạnh a. SO vuông góc với mặt phẳng (ABCD) và S O = a 2 Tính khoảng cách d giữa SC và AB.
A. d = a 3 5
B. d = a 5 5
C. d = a 2 3
D. d = 2 a 2 3