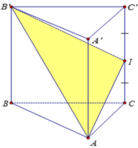
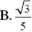
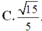
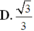
Cho khối lăng trụ đứng tam giác ABC.A'B'C' có đáy là một tam giác vuông cân tại A, AC = AB = 2a, góc giữa AC' và mặt phẳng (ABC) bằng 30 0 . Thể tích khối lăng trụ ABC.A'B'C' là
A . 4 a 3 3
B . 4 a 3 3 3
C . 2 a 3 3 3
D . 4 a 2 3 3
a) Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết diện tích tứ giác ABB'A' bằng \(2a^2\), thể tích khối lăng trụ ABC.A'B'C' bằng?
b) Cho hình lăng trụ đúng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết góc giữa (AB'C') và (A'B'C') bằng 60°, thể tích khối lăng trụ ABC.A'B'C' bằng?
a: BB'=2a^2:a=2a
V=BB'*S ABC
=2a*1/2a^2
=a^3
Lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác vuông cân tại A; A B = A C = a 5 ; A'B tạo với mặt đáy lăng trụ góc 60 ∘ . Thể tích khối lăng trụ bằng:
A. a 3 6
B. 5 a 3 15 2
C. 5 a 3 3 3
D. 4 a 3 6
Đáp án B
Ta có: A A ' ⊥ A B C ⇒ A ' B A ⏜ = A ' B ; A B C ^ = 60 ∘
Do đó A A ' = A B tan 60 ∘ = a 15 ; S A B C = A B 2 2 = 5 a 2 2
Suy ra V A B C . A ' B ' C ' = S h = 5 a 2 2 . a 15 = 5 a 3 15 2 .
Lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB =AC = a 5 , A'B tạo với mặt đáy lăng trụ góc 600. Tính thể tích khối lăng trụ.
A. a 3 6
B. 5 a 3 15 2
C. 5 a 3 3 3
D. 4 a 3 6
Lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A; AB=AC=a 5 ; A'B tạo với mặt đáy lăng trụ góc 60 0 . Thể tích khối lăng trụ bằng:
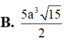
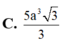
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân ABC với A B = A C = a , B A C ^ = 120 ° , mặt phẳng (AB'C') tạo với đáy một góc 30 ° . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 6
B. V = a 3 8
C. V = 3 a 3 8
D. V = 9 a 3 8
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân ABC với AB=AC=a,BAC= 120 o mặt phẳng (AB'C') tạo với đáy một góc 30 o Tính thể tích V của khối lăng trụ đã cho.
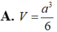
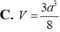
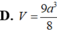
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB=AC=a, B A C ⏜ = 120 0 , mặt phẳng (A'B'C') tạo với đáy một góc 60 0 . Tính thể tích V của khối lăng trụ đã cho
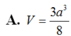
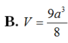
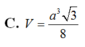
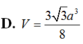
Cho khối lăng trụ đứng A B C . A ' B ' C ' có đáy là tam giác cân ABC với A B = A C = a , B A C ⏜ = 120 ° , mặt phẳng A B ' C ' tạo với đáy một góc 30 ° . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 6
B. V = a 3 8
C. V = 3 a 3 8
D. V = 9 a 3 8
Đáp án B
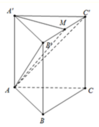
Ta có: S A B C = 1 2 A B . A C . sin A = a 2 3 4
Gọi M là trung điểm của B ' C ' khi đó
B ' C ' ⊥ A ' M B ' C ' ⊥ A A ' ⇒ B ' C ' ⊥ A ' M A
Suy ra A ' M A ⏜ = A B ' C ' ' A ' B ' C ' ⏜ = 30 °
Lại có A ' M = A ' B sin 30 ° = a 2 ⇒ A A ' = A ' M t a n 30 ° = a 2 3
⇒ V A B C . A ' B ' C ' = S A B C . A A ' = a 3 8
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB=AC=a, góc BAC=120o. Mặt phẳng (AB'C') tạo với đáy một góc 60o. Tính thể tích V của khối lăng trụ
Gọi H là trung điểm BC, H' là trung điểm B'C'
\(\left\{{}\begin{matrix}AH\perp BC\\AH\perp HH'\left(HH'\cap BC=\left\{H\right\}\right)\end{matrix}\right.\Rightarrow AH\perp\left(BCC'B'\right)\)
\(\widehat{\left(ABC\right),\left(AB'C'\right)=60^0\Rightarrow\widehat{H'AH}=60^0}\)
\(AH=\dfrac{a}{2}\Rightarrow HH'=AH\tan60^0=\dfrac{a\sqrt{3}}{2}\Rightarrow V=S_{ABC}.HH'=\dfrac{1}{2}.\sqrt{3}a.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{2}=\dfrac{3a^3}{8}\)
![[柠檬]๛Čɦαŋɦ ČŠツ](https://hoc24.vn/images/avt/avt6342624_256by256.jpg)
