Các câu hỏi tương tự
Cho khối lăng trụ đứng ABC.ABC có đáy là tam giác cân ABC với ABACa,BAC
120
o
mặt phẳng (ABC) tạo với đáy một góc
30
o
Tính thể tích V của khối lăng trụ đã cho.
Đọc tiếp
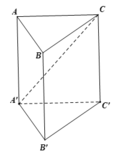
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân ABC với AB=AC=a,BAC= 120 o mặt phẳng (AB'C') tạo với đáy một góc 30 o Tính thể tích V của khối lăng trụ đã cho.
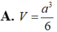
![]()
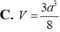
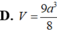
Cho hình lăng trụ ABC.ABC có đáy là tam giác đều cạnh 3a. Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là điểm D thỏa mãn
D
C
⇀
-
2
D
B
⇀
. Góc giữa đường thẳng AC’ và mặt phẳng (ABC) bằng
45
0
. Tính theo a thể tích khối lăng trụ ABC.ABC.
A
....
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh 3a. Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là điểm D thỏa mãn D C ⇀ = - 2 D B ⇀ . Góc giữa đường thẳng AC’ và mặt phẳng (A'B'C') bằng 45 0 . Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
A . 9 a 3 21 4
B . 3 a 3 21 4
C . 27 a 3 21 4
D . a 3 21 4
Cho hình lăng trụ đứng ABC.ABC, đáy ABC là tam giác vuông tại A, cạnh AA hợp với BC một góc
60
0
và khoảng cách giữa chúng bằng a, BC 2a. Thể tích của khối lăng trụ ABC.ABC theo a
A
.
a
3
2
B
.
3
a
3
2...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C', đáy ABC là tam giác vuông tại A, cạnh AA' hợp với B'C một góc 60 0 và khoảng cách giữa chúng bằng a, B'C = 2a. Thể tích của khối lăng trụ ABC.A'B'C' theo a
A . a 3 2
B . 3 a 3 2
C . 3 a 3 4
D . a 3 4
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại A, AB 2a. Biết diện tích tam giác ABC bằng 4
a
2
. Thể tích lăng trụ đó là:
A
.
2
10
a
3
3
B
.
2
10
a
3
C...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = 2a. Biết diện tích tam giác A'BC bằng 4 a 2 . Thể tích lăng trụ đó là:
A . 2 10 a 3 3
B . 2 10 a 3
C . 2 6 a 3
D . 2 6 a 3 3
Cho lăng trụ đứng ABC.A'B'C', có đáy ABC là tam giác vuông tại A, AB = 3a; AC = 4a, cạnh bên AA' = 2a. Tính thể tích của khối lăng trụ .
A. 12 a 3
B. 4 a 3
C. 3 a 3
C. 6 a 3
Cho khối lăng trụ đứng ABC.ABC có BBa đáy ABC là tam giác vuông cân tại B và AC
a
2
. Tính thể tích V của khối lăng trụ đã cho .
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có BB'=a đáy ABC là tam giác vuông cân tại B và AC= a 2 . Tính thể tích V của khối lăng trụ đã cho .
![]()
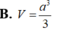
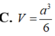
Cho lăng trụ tam giác đều ABC.ABC có cạnh đáy bằng a, góc giữa đường thẳng AC và mặt phẳng đáy bằng
60
0
. Tính thể tích khối lăng trụ ABC.ABC theo a.
A
.
3
a
3
4
B
.
a
3
12
C
.
...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, góc giữa đường thẳng AC' và mặt phẳng đáy bằng 60 0 . Tính thể tích khối lăng trụ ABC.A'B'C' theo a.
A . 3 a 3 4
B . a 3 12
C . 3 a 3 4
D . a 3 4
Cho lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại A, ABa, AC a
3
và BBCC là hình vuông. Khoảng cách giữa hai đường thẳng AA và BC là A.
a
3
2
B.
3
a
2
4
C. ...
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, AC =a 3 và BB'C'C là hình vuông. Khoảng cách giữa hai đường thẳng AA' và BC' là
A. a 3 2
B. 3 a 2 4
C. a
D. a 3
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân đỉnh C, AC a. Gọi x là góc giữa hai mặt phẳng (ACB) và (ABC) để thể tích khối chóp A.ABC lớn nhất. Tính thể tích lớn nhất của khối chóp A.ABC theo a A.
a
3
3
3
B.
a
3
3
9...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân đỉnh C, A'C = a. Gọi x là góc giữa hai mặt phẳng (A'CB) và (ABC) để thể tích khối chóp A'.ABC lớn nhất. Tính thể tích lớn nhất của khối chóp A'.ABC theo a
A. a 3 3 3
B. a 3 3 9
C. a 3 3 27
D. a 3 3 81