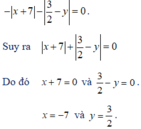Tìm y: y x 32 = 736

Những câu hỏi liên quan
Tìm y: y x 23 = 736
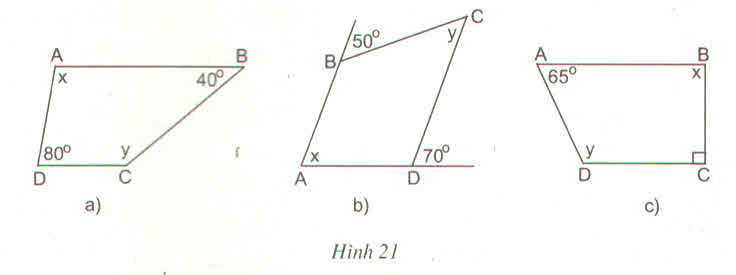
Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB và CD
a)
x = 1800 – 800 = 1000
y = 1800 – 400 = 1400
b)
x = 700 (đồng vị)
y = 500 (so le trong)
c)
x = 1800 – 900 = 900
y = 1800 – 650 = 1150
Đúng 0
Bình luận (0)
Bài giải:
a)
x = 1800 – 800 = 1000
y = 1800 – 400 = 1400
b)
x = 700 (đồng vị)
y = 500 (so le trong)
c)
x = 1800 – 900 = 900
y = 1800 – 650 = 1150
Đúng 0
Bình luận (0)
Bài 1:
a, Tìm y
123 - 3,5 x y = 53
y x 0,6 + y x 5 + y : 0,5 = 56,4
b, Tính bằng cách hợp lí
32 x 11 - 3200 x 0,1 : 32
17,2 x 8,5 + 0,46 x 17,2
Xem chi tiết
Tìm x,y thuộc Z : (y+1)^2 = 32.y/x
ta có \(\left(y+1\right)^2\)=\(\frac{32y}{x}\)=> x = \(\frac{32y}{\left(y+1\right)^2}\)=> x =\(\frac{16y^2+32y+16-16y^2-16}{\left(y+1\right)^2}\)=> x =\(\frac{16\left(y+1\right)^2-16\left(y^2-1\right)}{\left(y+1\right)^2}\)=> x = \(\frac{16\left(y+1\right)^2}{\left(y+1\right)^2}\)-\(\frac{16\left(y-1\right)\left(y+1\right)}{\left(y+1\right)^2}\)
=> x = 16 -\(\frac{16\left(y-1\right)}{y+1}\)=> x = 16 - \(\frac{16y+16-32}{y+1}\)=> x= 16-16 +\(\frac{32}{y+1}\)=> x= \(\frac{32}{y+1}\)
Vì x\(\in\)Z => \(\frac{32}{y+1}\)l \(\in\) Z => 32 \(⋮\)y+1 => y+1 \(\in\)Ư (32) = ( 1 ; 2;4;8;16;32;-1;-2;-4;-8;-16;-32)
đến đây dễ rồi tự làm
Đúng 1
Bình luận (0)
tìm x,y biết:
x+y=32 (x>y)
x-y=8
Minh chua biet cach lam
tìm 2 số x,y biết x/3=y/5vaf x+y=-32
Theo tính chất của dãy tỉ số bằng nhau ta có:
x/3=y/5=x+y/3+5=32/8=4
x/3=4=>x=4×3=12
y/5=4=>4×5=20
Vậy x=12;y=20
Đúng 0
Bình luận (0)
Tìm x, y thoả mãn: − x + 7 − 3 2 − y = 0
tìm hai số x,y biết : x trên 5 , y trên 3 và x+y=32
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/5=y/3=(x+y)/(5+3)=32/8=4`
`-> x/5=y/3=4`
`-> x=4*5=20, y=4*3=12`
Đúng 3
Bình luận (0)
Ta có `x/5 =y/3` và `x+y=32`
ADTC dãy tỉ số bằng nhau ta có :
`x/5=y/3 =(x+y)/(5+3)=32/8=4`
`=>x/5=4=>x=4.5=20`
`=>y=3=4=>y=4.3=12`
Vậy `x=20;y=12`
Đúng 2
Bình luận (1)
áp dụng dãy tỉ số bằng nhau ta có\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{8}=\dfrac{32}{8}=4\)do đó \(\dfrac{x}{3}=4=>x=12\)và \(\dfrac{y}{5}=4=>y=20\)vậy x=12 và y=20
Đúng 4
Bình luận (0)
tìm min \(A=32.\dfrac{x}{y}+2022.\dfrac{y}{x}\left(x,y>0;x+\dfrac{1}{y}< =1\right)\)
Từ giả thiết: \(1\ge x+\dfrac{1}{y}\ge2\sqrt{\dfrac{x}{y}}\Rightarrow\dfrac{x}{y}\le\dfrac{1}{4}\Rightarrow\dfrac{y}{x}\ge4\)
\(\Rightarrow A=2\left(\dfrac{16x}{y}+\dfrac{y}{x}\right)+\dfrac{2020y}{x}\ge2.2\sqrt{\dfrac{16xy}{xy}}+2020.4=8096\)
\(A_{min}=8096\) khi \(\left(x;y\right)=\left(\dfrac{1}{2};2\right)\)
Đúng 1
Bình luận (0)