Một vật dao động điều hòa theo phương trình x = 6 cos ( 4 πt + π 3 ) ( cm ) Lấy π 2 = 10 Gia tốc cực đại của vật là:
A. 24π cm/s2
B. 9,6 cm/s2.
C. 9,6 m/s2.
D. 24π2 cm/s2.
Vật dao động điều hòa với phương trình: x = 8cos(πt + π/6)cm. Pha ban đầu của dao động là
A. π 6 r a d
B. - π 6 r a d
C. ( π t + π 6 ) r a d
D. π 3 r a d
Đáp án A
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hòa
Pha ban đầu của dao động: φ = π 6 r a d
Một vật thực hiện đồng thời hai dao động thành phần: x1 = 10cos(πt + π/6)cm và x2 = 5 cos(πt + π/6)cm. Phương trình của dao động tổng hợp là:
A. x = 15cos(πt + π/6)cm.
B. x = 5cos(πt + π/6)cm.
C. x = 10cos(πt + π/6)cm.
D. x = 15cos(πt)cm.
Chọn A
+ Hai dao động cùng pha![]() và pha φ là pha của các dao động
và pha φ là pha của các dao động
=> x = 15cos(πt + π/6)cm.
Một vật dao động điều hòa với phương trình x = 10 cos ( π t + π 2 ) cm. Tần số góc của vật là
A. 0,5 (rad/s)
B. 2 (rad/s)
C. 0,5 π (rad/s)
D. π (rad/s)
Chất điểm có khối lượng m1 = 500gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 1 = cos ( 5 πt + π / 6 ) (cm). Chất điểm có khối lượng m2 = 100 gam dao động điều hòa quanh vị trí cân bằng của nó với phương trình dao động x 2 = 5 cos ( πt - π / 6 ) (cm). Tỉ số cơ năng trong quá trình dao động điều hòa của chất điểm m1 so với m2 bằng
A. 1/2.
B. 2.
C. 5.
D. 1/5.
Một vật khối lượng m = 100g thực hiện đồng thời 2 dao động điều hòa cùng phương theo các phương trình x 1 = A 1 cos(πt + φ 1 ) và x 2 = A 2 cos(πt + φ 2 )cm. Trong quá trình dao động luôn có 64 x 1 2 + 36 x 2 2 = 2304 ( cm 2 ). Lấy π 2 = 10. Cơ năng của vật bằn
A. 1,8mJ
B. 9,8mJ
C. 5mJ
D. 3,2mJ
Một vật thực hiện đồng thời ba dao động điều hoà cùng phương, cùng tần số có phương trình là x1,
x2, x3. Biết: x12 = 6cos(πt + π/6) cm; x23 = 6cos(πt + 2π/3) cm; x13 = 6 2 cos(πt + π/4) cm.Độ lệch pha của 2 dao động x2,x3?Khi li độ của dao động x1 đạt giá trị cực đại thì li độ của dao động x3 ?
Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
Một vật dao động điều hòa theo phương trình x = 20 cos ( 2πt +π/4 ) mm. Ở điểm t = 1/8 s li độ của vật là
Một vật dao động điều hòa có phương trình x = 4 cos(10πt + π/6) cm. Tại thời điểm t = 0 vật có tọa độ bằng bao nhiêu?
Một vật dao động điều hòa theo phương trình x = 10cos(πt + π/3 ) (cm/s). Kể từ lúc t = 0 thời điểm vận tốc của vật có độ lớn 5π (cm/s) lần thứ 21 là:
Trong `5` chu kì vật đi qua thời điểm vận tốc có độ lớn `5\pi(cm//s)` là `20` lần.
`=>1` lần vật đi trong: `\Delta t=T/12+T/6=T/4`
`=>` Kể từ `t=0` thời điểm vận tốc của vật có độ lớn `5\pi(cm//s)` lần thứ `21` là:
`t=T/4+5T=10,5(s)`.
Một vật thực hiện đồng thời ba dao động điều hòa cùng phương cùng tần số có li độ lần lượt là x1, x2, x3. Biết phương trình li độ tổng hợp của các dao động thành phần lần lượt là x 12 = 6 cos ( πt + π 6 ) x 23 = 6 cos ( πt + 2 π 3 ) x 13 = 6 2 cos ( πt + π 4 ) . Khi li độ của dao động x1 đạt giá trị cực tiểu thì li độ của dao động x3 là:
A. 0 cm.
B. 3 cm.
C. 3 6 c m
D. 3 2 c m
Từ giả thuyết bài toán, ta có:
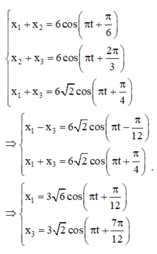
+ Hai dao động này vuông pha nhau. Ta có
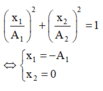
Đáp án A