Cho parabol ( P ) : y 2 = 2 x và đường tròn ( C ) : x 2 + y 2 = 8 . (P) chia (C) thành hai phần. Tìm tỉ số diện tích của hai phần đó.
A. 9 π + 2 3 π - 2
B. 9 π - 2 3 π - 2
C. 9 π + 2 3 π + 2
D. 9 π - 2 3 π + 2
Những câu hỏi liên quan
Bài 1 : Cho parabol ( P) : y x^2 và đường thẳng ( d) : y ( m+3).x - m+2 ( m là tham số ) a) Tìm điểm cố định mà điểm ( d ) đi qua với mọi giá trị mb) Chứng minh rằng với mọi m thì ( P) và ( d) 2OyBài 2 : Cho đường tròn ( O) với dây BC cố định và một điểm A thay đổi trên cung lớn BC sao cho AC AB và AC BC . Gọi D là điểm chính giữa của cung nhỏ BC . Các tiếp tuyến của ( O) tại D và C cắt nhau tại E . Gọi P, Q lần lượt là giao điểm của các cặp đường thẳng AB và CD ; AD với CEa) chứng minh rằn...
Đọc tiếp
Bài 1 : Cho parabol ( P) : y= \(x^2\) và đường thẳng ( d) : y= ( m+3).x - m+2 ( m là tham số )
a) Tìm điểm cố định mà điểm ( d ) đi qua với mọi giá trị m
b) Chứng minh rằng với mọi m thì ( P) và ( d) 2Oy
Bài 2 : Cho đường tròn ( O) với dây BC cố định và một điểm A thay đổi trên cung lớn BC sao cho AC > AB và AC > BC . Gọi D là điểm chính giữa của cung nhỏ BC . Các tiếp tuyến của ( O) tại D và C cắt nhau tại E . Gọi P, Q lần lượt là giao điểm của các cặp đường thẳng AB và CD ; AD với CE
a) chứng minh rằng : DE // BC
b) Chứng minh tứ giác PACQ nội tiếp đường tròn
( Ai giúp mình với mình cần gấp ạ )
Cho (H) là hình phẳng giới hạn bởi parabol y
3
x
2
và nửa đường tròn có phương trình y
4
-
x
2
với
-
2
≤
x
≤
2
(phần tô đậm trong hình vẽ). Diện tích của (H) bằng A.
2
π
+...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 với - 2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
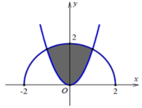
A. 2 π + 5 3 3
B. 4 π + 5 3 3
C. 4 π + 3 3
D. 2 π + 3 3
Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của 3 x 2 = 4 - x 2 <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2x ( ∫ 0 1 4 - x 2 d x - ∫ 0 1 3 x 2 d x ) = 2 π + 3 3
Đúng 0
Bình luận (0)
Cho (H) là hình phẳng giới hạn bởi parabol
y
3
x
2
và nửa đường tròn có phương trình
y
4
-
x
2
với
-
2
≤
x
≤
2
(phần tô đậm trong hình vẽ). Diện tích của (H) bằng A.
2
π
+
5...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 với - 2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
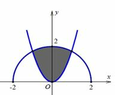
A. 2 π + 5 3 3
B. 4 π + 5 3 3
C. 4 π + 3 3
D. 2 π + 3 3
Cho
(
H
)
là hình phẳng giới hạn bởi parabol
y
3
x
2
và nửa đường tròn có phương trình
y
4
-
x
2
(với
-
2
≤
x
≤
2
) (phần tô đậm trong hình vẽ). Diện tích của
(
H
)
bằng A. ...
Đọc tiếp
Cho ( H ) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 (với - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của ( H ) bằng
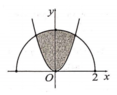
A. 2 π + 3 3
B. 4 π + 5 3 3
C. 2 π + 5 3 3
D. 4 π + 3 3
Bài 14 Cho parabol P y x 2 và đường thẳng d y 2m 1 x m 3 . Tìm m d hat e P và d cắt nhau tại hai điểm A, B nằm bên phải trục tùng, Bài 15 Cho parabol P y x 2 và đường thẳng d y a 1 x a . Tim a để P và d cắt nhau tại hai điểm phân biệt A và B sao cho tam giác AOB Bài 16 Cho Parabol P y x 2 và đường thẳng d y m 1 x m m là tham số . vuông tại O. Tim m d hat e đường thẳng d cắt parabol P tại hai điểm P và Q sao cho t...
Đọc tiếp
Bài 14 Cho parabol P y x 2 và đường thẳng d y 2m 1 x m 3 . Tìm m d hat e P và d cắt nhau tại hai điểm A, B nằm bên phải trục tùng, Bài 15 Cho parabol P y x 2 và đường thẳng d y a 1 x a . Tim a để P và d cắt nhau tại hai điểm phân biệt A và B sao cho tam giác AOB Bài 16 Cho Parabol P y x 2 và đường thẳng d y m 1 x m m là tham số . vuông tại O. Tim m d hat e đường thẳng d cắt parabol P tại hai điểm P và Q sao cho tam giác OPQ vuông tại Q.
Cho hàm số y -x² có đổ thị là parabol (P). a) Vẽ parabol (P) trên mặt phẳng tọa độ; b) Viết phương trinh đường thẳng (d), biết rằng (d) cắt parabol (P) tại điểm có hoành độ bằng 2 và cắt trục tung tại điểm có tung độ bằng 1. c) Hãy tìm góc tạo bởi đường thẳng (d) vừa xác định ở câu b) và trục Ox (làm tròn đến độ). Câu 3: (2,0 điểm) Cho phương trình ẩn x, tham số m: x² + (m- 1)x-m 0 a) Chứng minh phương trình luôn có nghiệm với mọi m; b) Tim m để phương trình có hai nghiệm x, X2; X X2 sao cho x...
Đọc tiếp
Cho hàm số y = -x² có đổ thị là parabol (P). a) Vẽ parabol (P) trên mặt phẳng tọa độ; b) Viết phương trinh đường thẳng (d), biết rằng (d) cắt parabol (P) tại điểm có hoành độ bằng 2 và cắt trục tung tại điểm có tung độ bằng 1. c) Hãy tìm góc tạo bởi đường thẳng (d) vừa xác định ở câu b) và trục Ox (làm tròn đến độ). Câu 3: (2,0 điểm) Cho phương trình ẩn x, tham số m: x² + (m- 1)x-m 0 a) Chứng minh phương trình luôn có nghiệm với mọi m; b) Tim m để phương trình có hai nghiệm x, X2; X < X2 sao cho x - 2x = -2. Câu 4: (2,0 điểm) Cho đường tròn (0; 6cm) và A là điểm nằm ngoài đường tròn (0) sao cho OA = 10cm. Qua A về các tiếp tuyến AB, AC với đường tròn (0) (B,C là các tiếp điểm); AO cắt BC tại H. a) Chứng minh tứ giác OBAC nội tiếp được; b) Tính độ dài đoạn thẳng BH; c) Vẽ đường kính BD của đường tròn (0). Chứng minh CD I OA
13 tháng 6 2021 lúc 8:55
cho đường thẳng (d): y=2mx+2m-3 và parabol (P): y=x^2 tìm m để đường thẳng tiếp xúc với parabol P
pt hoành độ giao điểm: \(x^2-2mx-2m+3=0\)
Để đường thẳng tiếp xúc với parabol thì pt có 1 nghiệm duy nhất
\(\Rightarrow\Delta'=0\)
\(\Delta'=m^2+2m-3=0\Rightarrow\left(m-1\right)\left(m+3\right)=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Câu 1: Cho parabol (P):y=x^2+bx+c (b,c là các tham số thực)
a. Tìm giá trị của b,c biết parabol (P) đi qua điểm M(-3;2) và có trục đối xứng là đường thẳng x=-1
b. Với giá trị của b,c tìm được ở câu a), tìm m để đường thẳng d:y=-x-m cắt parabol(P) tại 2 điểm phân biệt A,B sao cho tam giác OAB vuông tại O( với O là gốc toạ độ)
Cho parabol ( P ) : y = x2 và đường thẳng ( d ) : y = ( 2 -m )x + m2 + 1 .
a/ Vẽ parabol ( P ) .
b/ Chứng minh rằng parabol ( P ) và đường thẳng ( d ) luôn cắt nhau tại hai điểm phân biệt A và B .
b: Phương trình hoành độ giao điểm là:
\(x^2+\left(m-2\right)x-m^2-1=0\)
\(ac=-m^2-1< 0\)
Do đó: (P) luôn cắt (d) tại hai điểm phân biệt
Đúng 0
Bình luận (0)
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y - x2a) Vẽ parabol (P)b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y - x – 2 và (P).c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại MBài 2 Cho parabol (P): y x2 và đường thẳng (d): y x + mCMR: (d) luôn cắt (P) tại 2 điểm phân biệta) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P khi m thay đổiBài 3. Cho parabol (P): y x2 và đường...
Đọc tiếp
Bài 1. Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = - x2
a) Vẽ parabol (P)
b) Xác định tọa độ các giao điểm A, B của đường thẳng (d): y = - x – 2 và (P).
c) Tìm tọa độ điểm M trên (P) sao cho tam giác MAB cân tại M
Bài 2 Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
CMR: (d) luôn cắt (P) tại 2 điểm phân biệt
a) Giả sử (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ x1; x2. Hãy tìm giá trị nhỏ nhất của biểu thức P = 
khi m thay đổi
Bài 3. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Tìm m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt nằm bên phải trục tung
Bài 4. Cho parabol (P): y = x2 và đường thẳng (d): y = x + m
Bài 5. Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 1
Tìm m sao cho (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 sao cho 
Bài 6. Cho parabol (P) : y = 
x2 và đường thẳng (d) : y = mx - m2 + m +1.
a) Với m = 1, xác định tọa độ các giao điểm A, B của (d) và (P).
b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 sao cho 
.