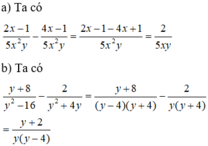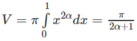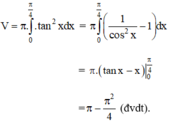Tính các tích phân sau: ∫ 0 1 y - 1 2 y d y , đặt t = y

Những câu hỏi liên quan
Tính thể tích khối tròn xoay đó hình phẳng giới hạn bởi các đường sau quay quanh Ox:
y = 1 - x 2 ; y = 0
Hoành độ giao điểm là nghiệm của phương trình :
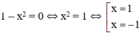
Vậy thể tích khối tròn xoay cần tính là:
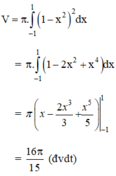
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
liên tục trên
0
;
1
thỏa mãn
∫
0
1
x
f
x
d
x
0
và
max
0
;
1
f...
Đọc tiếp
Cho hàm số y = f x liên tục trên 0 ; 1 thỏa mãn ∫ 0 1 x f x d x = 0 và max 0 ; 1 f x = 1. Tích phân I = ∫ 0 1 e x f x d x thuộc khoảng nào trong các khoảng sau đây?
A. − ∞ ; − 5 4
B. 3 2 ; e ; − 2
C. − 5 4 ; 3 2
D. e − 1 ; + ∞
Đáp án C

= ∫ 0 1 f x e x − α x d x ≤ ∫ 0 1 f x . e x − α x d x ≤ ∫ 0 1 e x − α x d x
⇒ ∫ 0 1 e x f x d x ≤ min α ∈ ℝ ∫ 0 1 e x − α x d x ≤ min α ∈ 0 ; 1 ∫ 0 1 e x − α x = min α ∈ 0 ; 1 e x − α x 2 2 0 1

Đúng 0
Bình luận (0)
Làm tính trừ các phân thức sau:a)
2
x
−
1
5
x
2
y
−
4
x
−
1
5
x
2
y
với
x
≠
0
và
y
≠
0
;b)...
Đọc tiếp
Làm tính trừ các phân thức sau:
a) 2 x − 1 5 x 2 y − 4 x − 1 5 x 2 y với x ≠ 0 và y ≠ 0 ;
b) y + 8 y 2 − 16 − 2 y 2 + 4 y với y ≠ 0 và y ≠ ± 4
Áp dụng phương pháp tính tích phân từng phần, hãy tính các tích phân sau:
∫
2
3
ln
x
-
1
-
ln
x
+
1
d
x
Đọc tiếp
Áp dụng phương pháp tính tích phân từng phần, hãy tính các tích phân sau: ∫ 2 3 ln x - 1 - ln x + 1 d x
Cho biểu thức sau đây : x - 2xy + y =0. Biết x và y là các số nguyên khác 0. tính tích của x; y
Cho A và D là hai chữ số khác 0 và số có hai chữ số tạo bởi các chữ số này có các tính chất sau: 1. DA có thể phân tích thành tích của 2 và một số nguyên tố khác; 2. AD có thể phân tích thành tích của 2 và một số nguyên tố khác. Nếu A>D, hãy tìm số có hai chữ số AD.
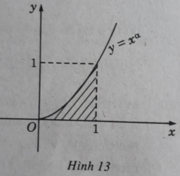
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = x α , α ∈ N*; y = 0; x = 0
Tính thể tích khối tròn xoay đó hình phẳng giới hạn bởi các đường sau quay quanh Ox: y = tanx; y = 0; x = 0; x = π 4
Bài 1: a) Tính 3x. (x-1)
b) Phân tích các đa thức sau thành nhân tử x3 - 2x2 + x
c) Tính giá trị biểu thức x2 - 2xy - 9z2 + y2 . Tại x = 6; y = -4; z = 30
a) 3x . ( x-1 ) = 3x2 - 3x
b) x3- 2x2+x = x2.( x-1 ) - x.( x-1 ) = (x-1).(x-1).x
= (x-1)2.x
c) x2- 2xy-9z2+y2
= (x2-2xy+y2 )-(3z)2
= (x-y)2-(3z)2
= ( x-y-3z).(x-y+3z)
thay vào ta có ( 6+4-90 ).(6+4+90 )=-80.100=-8000
Đúng 0
Bình luận (0)