Tiếp tuyến của đồ thị hàm số y = x 4 - 3 x 2 + 1 tại điểm cực tiểu của đồ thị có phương trình
A. y = - 5 4 x
B. y = - 5 4
C. y = 5 4 x
D. y = - 5 4
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 − 2 x 2 + 3 x − 5
A. Có hệ số góc dương
B. Song song với trục hoành
C. Có hệ số góc bằng -1
D. Song song với đường thẳng x = 1
Phương pháp:
+) Xác định điểm cực tiểu của đồ thị hàm số.
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm cực tiểu vừa tìm được và kết luận
Cách giải:

Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 - 2 x 2 + 3 x - 5
A. song song với đường thẳng x = 1
B. song song với trục hoành
C. có hệ số góc dương
D. có hệ số góc bằng -1
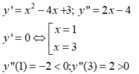
Do đó, hàm số đã cho đạt cực tiểu tại điểm x = 3 => y = -5
Phương trình tiếp tuyến tại điểm cực tiểu là:
y = 0(x - 3) – 5 = -5
Đây là đường thẳng song song với trục hoành,
Chọn B.
Viết phương trình tiếp tuyến của đồ thị hàm số y = - x 4 + 6 x 2 - 5 tại điểm cực tiểu của nó
A. y = 5
B. Y = - 5
C. y = 0
D. y = x + 5
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 - 2 x 2 + 3 x - 5 là đường thẳng
A. song song với đường thẳng x = 1
B. song song với trục hoành
C. có hệ số góc dương.
D. có hệ số góc bằng -1
Đáp án B.
Ta có: y’ = x2 – 4x + 3;
y' = 0 ó x= 3 hoặc x= 1
Bảng biến thiên:
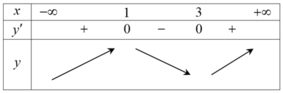
Hàm số đạt cực tiểu tại điểm M(3;-5).
y'(3) = 0;
Phương trình tiếp tuyến là: y = 0(x – 3) – 5 ó y = -5
Đường thẳng này song song với trục hoành.
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 - 2 x 2 + 3 x - 5 là đường thẳng:
A. Có hệ số góc dương.
B. Có hệ số góc âm.
C. Song song với trục hoành.
D. Song song với đường thẳng y = - 5
Chọn đáp án C
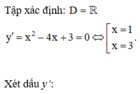
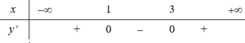
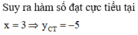
=> Phương trình tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là y = -5
Vậy tiếp tuyến tại điểm cực tiểu của đồ thị hàm số song song với trục hoành.
MEMORIZE
Tiếp tuyến (nếu có) tại các điểm cực trị của đồ thị hàm số bất kì là các đường thẳng song song hoặc trùng với trục hoành.
Xét các khẳng định sau:
(I). Nếu hàm số y = f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M > m
(II). Đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III). Tiếp tuyến (nếu có) tại một điểm cực trị của đồ thị hàm số luôn song song với trục hoành.
Số khẳng định đúng là :
A. 0
B. 3
C. 2
D. 1
Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
(I) sai. Ví dụ hàm số 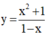 có đồ thị hàm số như sau:
có đồ thị hàm số như sau:
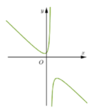 õ ràng
õ ràng ![]()
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số ![]() => Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là:
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: ![]() luôn song song với trục hoành.
luôn song song với trục hoành.
Vậy (III) đúng.
Gọi ∆ là tiếp tuyến tại điểm cực tiểu của đồ thị hàm số y = 1 3 x 3 - 2 x 2 - 5 Khẳng định nào sau đây đúng?
A. ∆ song song với trục hoành
B. ∆ có hệ số góc dương.
C. ∆ có hệ số góc bằng –1.
D. song song với đường thẳng y = - 5
Đáp án là A.
• Ghi chú: Tiếp tuyến tại điểm cực trị của hàm số bậc 3 song song với trục hoành.
Ta có: + y , = x 2 - 4 x + 3 ; y , = 0 ⇔ x = 1 x = 3
+ y , , = 2 x - 4 ; y , , ( 3 ) = 2 > 0 Hàm số đạt cực tiểu tại x = 3 ⇒ y = - 5
Phương trình tiếp tuyến là y = - 5 . Vậy tiếp tuyến song song với trục hoành.
Viết phương trình tiếp tuyến của đồ thị hàm số:
\(y=\dfrac{-x+2}{x+1}\)
a, Tại giao điểm của đồ thị vs trục hoành
b, Tại giao điểm của đồ thị vs trục tung
c, Hệ số góc \(k=-3\)
Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm
Ta có: y' \(=\dfrac{-3}{\left(x+1\right)^2}\)
k=f'\(\left(x_0\right)\)\(\Rightarrow-3=\dfrac{-3}{\left(x_0+1\right)^2}\Leftrightarrow\left(x_0+1\right)^2=1\)\(\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-2\end{matrix}\right.\)
Với \(x_0=0\) ta có pt tiếp tuyến:
\(d:3x+y-2=0\)
Với \(x_0=-2\) ta có pt tiếp tuyến:
\(d:3x+y+10=0\)
a: Tọa độ giao điểm của (d) với trục Ox là:
y=0 và (-x+2)=0
=>x=2 và y=0
\(y'=\dfrac{\left(-x+2\right)'\left(x+1\right)-\left(-x+2\right)\left(x+1\right)'}{\left(x+1\right)^2}\)
\(=\dfrac{\left(-\left(x+1\right)+x-2\right)}{\left(x+1\right)^2}=\dfrac{-3}{\left(x+1\right)^2}\)
Khi x=2 thì y'=-3/(2+1)^2=-3/9=-1/3
y-f(x0)=f'(x0)(x-x0)
=>y-0=-1/3(x-2)
=>y=-1/3x+2/3
b: Tọa độ giao của (d) với trục Oy là;
x=0 và y=(-0+2)/(0+1)=2
Khi x=0 thì \(y'=\dfrac{-3}{\left(0+1\right)^2}=-3\)
y-f(x0)=f'(x0)(x-x0)
=>y-2=-3(x-0)
=>y=-3x+2
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$