Hãy viết các công thức tính diện tích tam giác theo một cạnh và đường cao tương ứng.

Những câu hỏi liên quan
Cho tam giác MNP có đường cao PQ (Hình 17).a) Viết công thức tính PQ theo cạnh n và góc a; công thức tính PQ theo cạnh m và góc bb) Viết công thức tính diện tích mỗi tam giác MPQ, NPQ, MNP theo các cạnh m, n và các cạnh m, n và các góc a, b, a + bc) Sử dụng kết quả: {S_{MPN}} {S_{MPQ}} + {S_{NPQ}}, hãy tìm công thức tính sin left( {a + b} right) theo sin a,cos a,sin b,cos b. Từ đó rút ra đẳng sin left( {a + b} right) sin acos b + cos asin b,,,left( * right)d) Tính sin left( {a...
Đọc tiếp
Cho tam giác MNP có đường cao PQ (Hình 17).

a) Viết công thức tính PQ theo cạnh n và góc a; công thức tính PQ theo cạnh m và góc b
b) Viết công thức tính diện tích mỗi tam giác MPQ, NPQ, MNP theo các cạnh m, n và các cạnh m, n và các góc a, b, a + b
c) Sử dụng kết quả: \({S_{MPN}} = {S_{MPQ}} + {S_{NPQ}}\), hãy tìm công thức tính \(\sin \left( {a + b} \right)\) theo \(\sin a,\cos a,\sin b,\cos b\). Từ đó rút ra đẳng \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\,\,\,\left( * \right)\)
d) Tính \(\sin \left( {a - b} \right)\) bằng cách biến đổi \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right]\) và sử dụng công thức (*)
a) \(PQ = n.\cos a,PQ = m.\cos b\)
b) \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)
\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)
c) \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)
\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)
d) \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right] = \sin a.\cos \left( { - b} \right) + \cos a.\sin \left( { - b} \right) = \sin a.\cos b - \cos a.\sin b\)
Đúng 0
Bình luận (0)
Tam giác vuông ABC có
∠
A
90
0
và đường cao AH. Từ H hạ HK vuông góc vói AC. Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.
Đọc tiếp
Tam giác vuông ABC có ∠ A = 90 0 và đường cao AH. Từ H hạ HK vuông góc vói AC. Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.
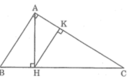
Các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng:
-
△
ABC đồng dạng
△
HBA. Ta có: 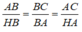
-
△
ABC đồng dạng
△
HAC. Ta có: 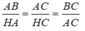
-
△
ABC đồngdạng
△
KHC. Ta có: 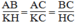
-
△
ABC đồng dạng
△
KAH. Ta có: 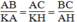
-
△
HBA đồng dạng
△
HAC. Ta có: 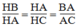
-
△
HBA đồng dạng
△
KHC. Ta có: 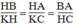
-
△
HBA đồng dạng
△
KAH. Ta có: 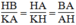
-
△
HAC đồng dạng
△
KHC.Ta có: 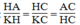
-
△
HAC đồng dạng
△
KAH. Ta có: 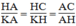
-
△
KHC đồngdạng
△
KAH. Ta có: 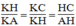
Đúng 0
Bình luận (0)
Cho tam giác abc toạ độ được nhập từ bàn phím các đường cao tương ứng ha,hb,hc độ dài cạnh ab=c , ac=b ,bc=a tính và đưa ra màng hình 1) tính và đưa ra màng hình diện tích tam giác theo công thứ hê rông 2)tính và đưa ra màng hình độ dài các đường cao ha,hb,hc
a) Một hình chữ nhật có diện tích 12 cm2. Viết công thức biểu thị sự phụ thuộc giữa một cạnh có độ dài y (cm) và cạnh kia có ddoooj dài x (cm) của hình chữ nhật.
b) Một tam giác có diện tích 10 cm2. Viết công thức biểu thị sự phụ thuộc giữa một cạnh có độ dài y (cm) và đường cao tương ứng có độ dài x (cm) của tam giác đó.
A...gọi hai cạnh của một hình chữ nhật lần lượt là x và y
do hình chữ nhật có diện tích là x.y= 12 (cm2 )nên công thức biểu thị sự phụ thuộc giữa một cạnh có độ dài y (cm) và cạnh kia có độ dài x (cm) của hình chữ nhật là y=\(\frac{12}{x}\)
B...gọi tương tự với cạnh đó và đường cao của nó
do diện tích của hình tam giác là \(\frac{1}{2}\)x.y=10(cm2) nên công thức biểu thị sự phụ thuộc giữa một cạnh có độ dài y (cm) và đường cao tương ứng có độ dài x (cm) của tam giác đó.là y=\(\frac{20}{x}\)
Một tấm bìa hình tam giác có cạnh đáy là 32cm và chiều cao tương ứng ngắn hơn cạnh đáy 7cm. Tính diện tích tấm bìa đó.
Các bạn nhớ ghi công thức tính cho mình nha!
Chiều cao tấm bìa là:
32 - 7 = 25 (cm)
Diện tích tấm bìa là:
32 x 25 : 2 = 400 (cm2)
đáp số : 400 cm2
Công thức : S = a x h : 2 ( s là diện tích ; a là độ dài đáy ; h là chiều cao)
Một mảnh đất hình chữ nhật có chiều dài 22,5 , chiều rộng 7,5m. Người ta dành 80% diện tích đất để làm nhà. Tính diện tích đất dùng để làm nhà.
Các bạn hãy ghi công thức tính cho mình nha!
chỉ ghi công thức thôi à
Xem thêm câu trả lời
Tính diện tích tam giác với độ dài canh a và đường cao h tương ứng.
a, Xác định bài toán, mô tả thuật toán.
b, viết đoạn chương trình tính diện tích với công thức S= ( a.h) :2
Xem chi tiết
Input: chiều cao h và cạnh a
Output: diện tích hình tam giác
Đúng 0
Bình luận (0)
B1: nhập 2 cạnh a,h
B2: s:=(a*h)/2;
B3: in ra màn hình
B4: kết thúc ct
Đúng 0
Bình luận (0)
Một tam giác có diện tích 6cm2. Công thức biểu thị sự phụ thuộc giữa một cạnh có độ dài y(cm) và đường cao tương ứng có độ dài x(cm) của tam giác đó là:
Ta có :
2S = xy =2.6=12
=>y=12/x
tick mik vs nha!!![]()
Đúng 0
Bình luận (0)
em hãy viết chương trình tính diện tích hình tam giác với độ dài cạnh và chiều cao tương ứng được nhập từ bàn phím
Uses crt;
Var a, h:real;
Begin
Readln(a);
Readln(h);
Writeln(a*h/2);
Readln
End.
Đúng 1
Bình luận (1)
Diện tích của một tam giác là 27cm2, biết rằng tỉ số giữa một cạnh và đường cao tương ứng của tam giác là 1,5. tính độ dài cạnh và đường cao nói trên?
giả sử đường cao là a thì cạnh tương ứng với nó sẽ là 1,5a (a >0)
diện tích tam giác là S = 1/2 .a.1,5a = 3/4.a2 = 27 => a 2 = 36 => a = 6
1,5a = 9
vậy cạnh của tam giác là 9 cm và đường cao tương ứng là 6 cm
Đúng 1
Bình luận (0)
cạnh / đường cao = 1,5 => cạnh = 1,5. đường cao
S = 1/2.cạnh.đường cao = 1/2 . 1,5 đường cao . đường cao = 27 cm2
đường cao 2 = 36
đường cao = 6
cạnh = 1,5 . 6 = 9
Đúng 0
Bình luận (0)
Gọi độ dài cạnh và đường cao nói trên lần lượt là a;b (a;b > 0)
1,5 = \(\frac{3}{2}\)
Ta có \(\frac{a}{b}=\frac{3}{2}\) => \(\frac{a}{3}=\frac{b}{2}\)
Đặt \(\frac{a}{3}=\frac{b}{2}=k\) => a = 3k; b = 2k
Ta có \(\frac{ab}{2}=27\) => ab = 27.2 = 54 => 3k2k = 54 => 6k2 = 54 => k2 = 9 => k = +3
=> a = 3.(+3) = + 9; b = 2.(+3) = +6
mà a;b > 0 nên a = 9; b = 6
Vậy độ dài cạnh và đường cao nói trên lần lượt là 9cm; 6cm
Đúng 0
Bình luận (0)





















