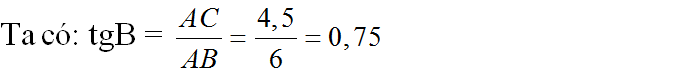Cho tam giác ABC có: AB = 4,5cm , BC = 6cm , AC = 7,5 .Chứng tỏ tam giác ABC là tam giác vuông

Những câu hỏi liên quan
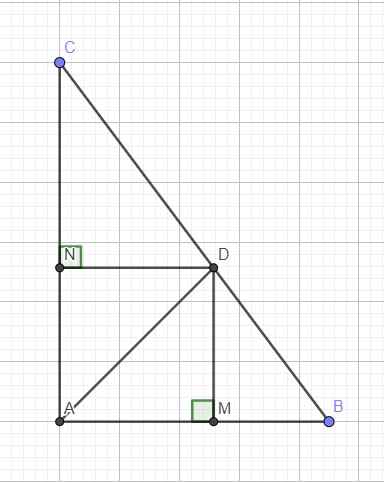
Cho tam giác ABC có AB=4,5cm AC=6cm và BC=7,5 cm a)Chứng minh rằng tam giác ABC vuông b)Kẻ phân giác AD. Gọi M và N lầ lượt là hình chiếu vuông góc của D trên AB và AC. Tính diện tích tứ giác AMDN
a.
\(AB^2+AC^2=4,5^2+6^2=56,25\)
\(BC^2=7,5^2=56,25\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A theo Pitago đảo
b.
Theo định lý phân giác: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow DB=\dfrac{3}{4}DC\)
Mà \(DB+DC=BC=7,5\)
\(\Rightarrow\dfrac{3}{4}DC+DC=7,5\Rightarrow DC=\dfrac{30}{7}\left(cm\right)\)
Do DN và AB cùng vuông góc AC \(\Rightarrow DN||AB\)
Áp dụng định lý Talet:
\(\dfrac{DN}{AB}=\dfrac{DC}{BC}=\dfrac{4}{7}\Rightarrow DN=\dfrac{4}{7}AB=\dfrac{18}{7}\left(cm\right)\)
Tứ giác AMDN là hình chữ nhật (có 3 góc vuông)
Mà AD là đường chéo đồng thời là phân giác theo giả thiết
\(\Rightarrow AMDN\) là hình vuông
\(\Rightarrow S_{AMDN}=DN^2=\dfrac{324}{49}\approx6,6\left(cm^2\right)\)
Đúng 2
Bình luận (1)
a) Xét ΔABC có \(BC^2=AB^2+AC^2\left(7.5^2=4.5^2+6^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Đúng 1
Bình luận (0)
Cho tam giác ABC có BC=7,5 cm AC=4,5cm AB=6cm . Tam giác ABC là tam giác gì ?
Áp dụng định lí Py-ta-go,ta có:
BC2=AC2+AB2
=4,52+62
=20,25+36
=56,25
mà\(\sqrt{56,25}\)=7,5
Suy ra tam giác ABC là tam giác vuông.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB= 4,5cm; BC= 6cm; AC= 7,5cm. Chứng minh tam giác ABC là tam giác vuông
Áp dụng ĐL pi - ta - go đảo :
\(AB^2+BC^2=AC^2\)
\(< =>4.5^2+6^2=7.5^2\)
Do \(4.5^2+6^2=7.5^2\)đúng
=>ĐPCM
cho tam giác ABC: AB =4,5cm ; AC=6cm ;BC=7,5cm a) chứng tỏ rằng BC²=AB²+AC² b) tam giác ABC là tam giác gì? Vì sao? c) vẽ trung tuyến AM, kẻ AH vuông AC.Trên tia đối của MH lấy điểm K sao cho MK=MH chứng minh : tam giác MHC = tam giác MKB d) chứng minh : BK //AC
Bạn nào giúp mình với chiều mình phải nộp rồi
a: \(BC^2=7.5^2=56.25\)
\(AB^2+AC^2=4.5^2+6^2=56.25\)
Do đó: \(BC^2=AB^2+AC^2\)
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét ΔMHC và ΔMKB có
MH=MK
\(\widehat{HMC}=\widehat{KMB}\)
MC=MB
Do đó: ΔMHC=ΔMKB
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB = 6cm, AC = 4,5cm. BC = 7,5 cm
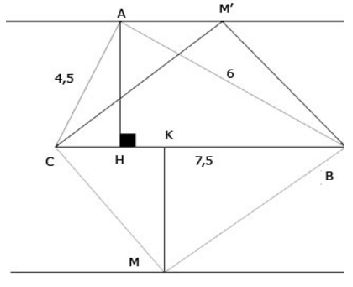
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào ?
b)Để SMBC = SABC thì M phải cách BC một khoảng bằng AH. Do đó M phải nằm bên trên hai đường thẳng song song với BC, cách BC một khoảng bằng 3,6cm.
Đúng 0
Bình luận (0)
Lời giải:
b)Để SMBC = SABC thì M phải cách BC một khoảng bằng AH. Do đó M phải nằm bên trên hai đường thẳng song song với BC, cách BC một khoảng bằng 3,6cm.
Đúng 0
Bình luận (0)
Bài 7:
Cho ∆ABC, Kẻ AH vuông góc BC (HBC), biết AH = 6cm, BH = 4,5cm, HC = 8cm.
a) Tính AB và AC
b) Chứng tỏ tam giác ABC là tam giác vuông.
a: \(AB=\sqrt{AH^2+HB^2}=7.5\left(cm\right)\)
\(AC=\sqrt{AH^2+HC^2}=10\left(cm\right)\)
BC=HB+HC=12,5cm
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. Chứng minh tam giác ABC vuông ở A. Tính các góc B , C và đường cao AH của tam giác
Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
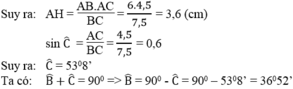
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
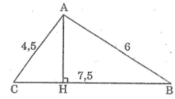
Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
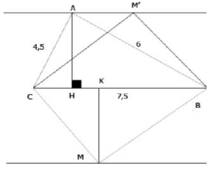
Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2
nên tam giác ABC vuông tại A. (đpcm)
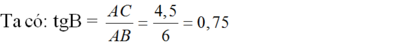
=> ∠B = 37o
=> ∠C = 90o - ∠B = 90o - 37o = 53o
Mặt khác trong tam giác ABC vuông tại A, ta có:
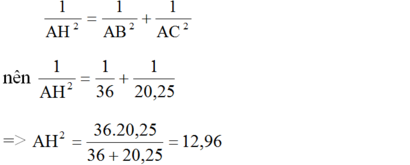
=> AH = 3,6 cm
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC có hai cạnh góc vuông AB = 4,5cm, AC= 6cm, cạnh huyền BC = 7,5cm. Tính chiều cao AH của hình tam giác vuông ABC.
TK
Diện tích tam giác là:
(4,5 x 6)/2=13,5 cm
Chiều cao AH là:
(13,5 x 2)/7,5=3,6 cm
Đúng 1
Bình luận (0)