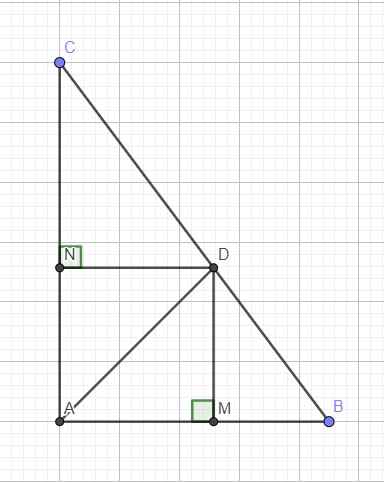
a.
\(AB^2+AC^2=4,5^2+6^2=56,25\)
\(BC^2=7,5^2=56,25\)
\(\Rightarrow AB^2+AC^2=BC^2\Rightarrow\Delta ABC\) vuông tại A theo Pitago đảo
b.
Theo định lý phân giác: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow DB=\dfrac{3}{4}DC\)
Mà \(DB+DC=BC=7,5\)
\(\Rightarrow\dfrac{3}{4}DC+DC=7,5\Rightarrow DC=\dfrac{30}{7}\left(cm\right)\)
Do DN và AB cùng vuông góc AC \(\Rightarrow DN||AB\)
Áp dụng định lý Talet:
\(\dfrac{DN}{AB}=\dfrac{DC}{BC}=\dfrac{4}{7}\Rightarrow DN=\dfrac{4}{7}AB=\dfrac{18}{7}\left(cm\right)\)
Tứ giác AMDN là hình chữ nhật (có 3 góc vuông)
Mà AD là đường chéo đồng thời là phân giác theo giả thiết
\(\Rightarrow AMDN\) là hình vuông
\(\Rightarrow S_{AMDN}=DN^2=\dfrac{324}{49}\approx6,6\left(cm^2\right)\)
a) Xét ΔABC có \(BC^2=AB^2+AC^2\left(7.5^2=4.5^2+6^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)