Cho elíp E : x 2 16 + y 2 9 = 1 và đường thẳng d: 3x+ 4y -12= 0. Số giao điểm của đường thẳng d và elip (E) là:
A. 0
B.1
C. 2
D. 3
Cho elíp E : x 2 25 + y 2 9 = 1 và đường thẳng d: x- 2y +12= 0. điểm M trên (E) sao cho khoảng cách từ điểm M đến đường thẳng d là lớn nhất, nhỏ nhất.Tìm GTLN; GTNN đó?
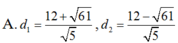
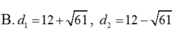
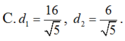
D. Đáp án khác
Đáp án A
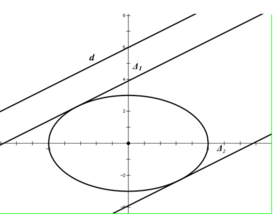
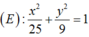 có độ dài nửa trục lớn a = 5và độ dài nửa trục bé b= 3
có độ dài nửa trục lớn a = 5và độ dài nửa trục bé b= 3
Gọi ![]() là tiếp tuyến của (E) mà
là tiếp tuyến của (E) mà ![]() song song với d
song song với d
=> x- 2y + C = 0.
Vì d tiếp xúc với (E) nên ta có:
![]()
Nên ta có hai tiếp tuyến của (E) song song với d là:
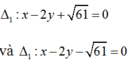
Vậy khoảng cách từ M đến đường thẳng d là lớn nhất là:
 , khoảng cách từ M đến đường thẳng d là bé nhất là:
, khoảng cách từ M đến đường thẳng d là bé nhất là:
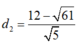
Trong mặt phẳng với hệ tọa độ Oxy, cho elíp : E : x 2 4 + y 2 = 1 và điểm C( 2;0) .Tìm tọa độ các điểm A; B trên (E), biết rằng hai điểm đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều và điểm A có tung độ dương .
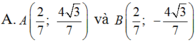
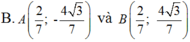
![]()
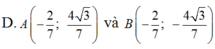
Đáp án A
Giả sử A( x0 ; y0) , Do A ; B đối xứng nhau qua Ox nên B( x0 ; -y0).
Ta có:
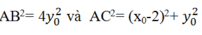
Vì A thuộc (E) nên:
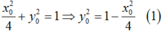
Vì AB = AC nên:
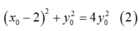
Thay (1) vào (2) ta được:
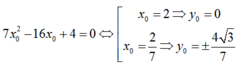
Vì điểm A khác C và Acó tung độ dương nên:
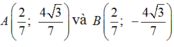
Cho hai elíp E 1 : x 2 9 + y 2 4 = 1 v à E 2 : x 2 16 + y 2 1 = 1 Gọi E 1 ∩ E 2 = A , B , C , D Lập phương trình đường tròn ngoại tiếp hình chữ nhật ABCD.
A.11x2+ 11y2= 92
B. x2+ y2= 1
C. x2+ y2= 11
D. tất cả sai
Đáp án A
Xét hệ:

Đường tròn ngoại tiếp hình chữ nhật ABCD có tâm O và bán kính

Vậy phương trình đường tròn cần tìm là:

Cho (E): \(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\), tiêu điểm F1, F2. Cho A, B là 2 điểm thuộc (E) sao cho AF1+BF2=8. Tính AF2+BF1
Cho tổng: A = 12+ 14+ 16 + x với x E N. Tìm x để
a) A chia hết cho 2
b) A không chia hết cho 2
A=42+x
a) số chia hết cho 2 tận cùng là số 2
=>x là số tự nhiên chẵn.
b)x là số lẻ
a) số chia hết cho 2 tận cùng là số chẵn
a, vì 12 chia hết cho 2
14 chia hết cho 2
16 chia hết cho 2=>để A chia hết cho 2 thì x chia hết cho 2
=> x=2k
1) Trong mat phang toa do Oxy , cho elip (E) : \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) va vecto v = (2;1). Anh cua (E)qua phep tinh tien T la:
Cho A= 16 + 48 + 72 + x (x E N)
a. Tìm điều kiện của x để A chia hết cho 2
b. Tìm điều kiện của x để A không chia hết cho 2
Vì 16 chia hết cho 2, 48 chia hết cho 2 và 72 chia hết cho 2
a) Để A chia hết cho 2 thì x phải chia hết cho 2.Vậy x có dạng 2k (k E N)
b) Để A không chia hết cho 2 thì x phải không chia hết cho 2. Vậy x có dạng 2k+1 (k E N)
Cho tổng : A = 12 + 14 + 16+ x với x E N . Tìm x để :
a) A chia hết cho 2
b) A ko chia hết cho 2
9 x 8 x 48 + 7 x 4 x 48 + 72 x 52
=72 x 48 + 28 x 48 + 72 x 52
=( 72 + 28 ) x 48 + 72 x 52
=100 x 48 + 3744
=4800 + 3744
=8544
a) Vì tổng (12 + 14 + 16) là số chẵn nên x là số chẵn thì A chia hết cho 2
b) x lẻ thì A sẽ ko chia hết cho 2
a,(x-4).(x+3)=0
b,(x^2+16).(x^2-16)=0
c,(x^2+10).(x-3)<0
d,(-x^2-9).(2-x)<0
e,(x-2).(x+4)=0
Lam nhung cau cac ban biet nhe
Ai lam dung minh tick tick tick cho
a) \(\left(x-4\right)\left(x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-4=0\\x+3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=4\\x=-3\end{cases}}\)
Vậy \(x\in\left\{-3;4\right\}\)
b)\(\left(x^2+16\right)\left(x^2-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+16=0\\x^2-16=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{-16}\\x=\sqrt{16}=4\end{cases}}\)
Vậy \(x=4\)
\(\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=-3\end{cases}}\)
\(\left(x^2+16\right)\left(x^2-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+16=0\\x^2-16=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=-16\left(loại\right)\\x^2=16\end{cases}}\Rightarrow x=\left(\pm4\right)^2\)
\(\left(x-2\right)\left(x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+4=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=-4\end{cases}}\)
c) \(\left(x^2+10\right)\left(x-3\right)< 0\)
\(\Rightarrow\hept{\begin{cases}x^2+10\\x-3\end{cases}}\)trái dấu
TH1 : \(\hept{\begin{cases}x^2+10>0\\x-3< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2>-10\\x< 3\end{cases}}\Leftrightarrow\hept{\begin{cases}x\inℤ\\x< 3\end{cases}}\Leftrightarrow x\in\left\{...;1;2\right\}\)
TH2 : \(\hept{\begin{cases}x^2+10< 0\\x-3>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2< -10\\x>3\end{cases}}\Leftrightarrow\hept{\begin{cases}x\in\varnothing\\x>3\end{cases}}\Leftrightarrow x\in\left\{\varnothing\right\}\)
\(\Rightarrow x\in\left\{...;1;2\right\}\)