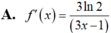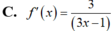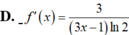Đạo hàm của hàm số f(x) = log3( 3x+1) là:
A. ![]()
B. 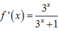
C. 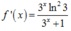
D. 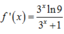
Hàm số f ( x ) = log 3 ( sin x ) có đạo hàm là
A. f ' ( x ) = c o t x ln 3
B. f ' ( x ) = tan x ln 3
C. f ' ( x ) = c o t x . ln 3
D. f ' ( x ) = 1 sin x . ln 3
Cho hàm số \(f(x) = {2^{3x + 2}}\)
a) Hàm số f(x) là hàm hợp của hàm số nào?
b) Tìm đạo hàm của f(x)
a) Hàm số f(x) là hàm hợp của hàm số \(y = {a^x}\)
b) \(f'(x) = \left( {{2^{3x + 2}}} \right)' = \left( {3x + 2} \right)'{.2^{3x + 2}}.\ln 2 = {3.2^{3x + 2}}.\ln 2\)
Hàm số y = l o g 3 ( x 3 – x ) có đạo hàm là
A. y ' = 3 x 2 - 1 ( x 3 - x ) l n 3
B. y ' = 3 x 2 - 1 ( x 3 - x )
C. y ' = 1 ( x 3 - x ) l n 3
D. y ' = 3 x - 1 ( x 3 - x ) l n 3
Hàm số y = log 3 ( x 3 - x ) có đạo hàm là
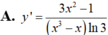
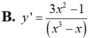
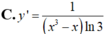
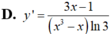
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Tính đạo hàm của hàm số y= log 3 ( x 2 - 1 ) .
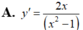
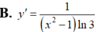
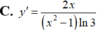
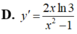
Cho hàm số y = f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm f’(x) .
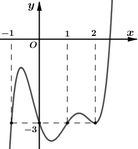
Hỏi hàm số y= g( x) = f( x) + 3x có bao nhiêu điểm cực trị ?
A. 2.
B. 3.
C. 4.
D. 7.
Cho f ( x ) = 3 x . 2 x . Khi đó, đạo hàm f’(x) của hàm số là
A. f ’ ( x ) = 3 x . 2 x . l n 2 . l n 3
B. f ’ ( x ) = 6 x l n 6
C. f ’ ( x ) = 2 x l n 2 - 3 x l n x
D. f ’ ( x ) = 2 x l n 2 + 3 x l n x
Tính đạo hàm f'(x) của hàm số f(x)= log 2 ( 3 x - 1 ) với x>1/