Cho hàm số f ( x ) = x + x 2 + 1 . Tập các giá trị của x để 2 x . f ' ( x ) - f ( x ) ≥ 0 là:
A. 1 3 ; + ∞
B. - ∞ ; 1 3
C. [ 2 3 ; + ∞ )
D. [ 1 3 ; + ∞ )
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
1) đạo hàm của hàm số \(\dfrac{2x^2+1}{x^2}\) là
2) cho hàm số \(f\left(x\right)=\sqrt{-5x^2+14x-9}\) tập hợp các giá trị của x để f'(x) = 0 là
1) \(y=\dfrac{2x^2+1}{x^2}\)
\(\Rightarrow y'=\dfrac{\left(4x+1\right)x^2-2x\left(2x^2+1\right)}{x^4}\)
\(\Leftrightarrow y'=\dfrac{4x^3+x^2-4x^3-2x}{x^4}\)
\(\Leftrightarrow y'=\dfrac{x^2-2x}{x^4}=\dfrac{x\left(x-2\right)}{x^4}=\dfrac{x-2}{x^3}\)
2) \(f\left(x\right)=\sqrt[]{-5x^2+14x-9}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-10x+14}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-2\left(5x-7\right)}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}\)
Để \(f'\left(x\right)=0\)
\(f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}=0\)
\(\Leftrightarrow5x-7=0\)
\(\Leftrightarrow5x=7\)
\(\Leftrightarrow x=\dfrac{7}{5}\)
Vậy tập hợp giá trị để \(f'\left(x\right)=0\) là \(\left\{\dfrac{7}{5}\right\}\)
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Cho hàm số f ( x ) = x + x 2 + 1 . Tập các giá trị của x để 2 x . f ' ( x ) - f ( x ) ≥ 0 là:
A. 1 3 ; + ∞
B. - ∞ ; 1 3
C. [ 2 3 ; + ∞ )
D. [ 1 3 ; + ∞ )
Đáp án D
- Phương pháp: Sử dụng công thức 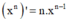 và
và 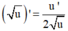 tính f'(x). Từ đó giải bất phương trình.
tính f'(x). Từ đó giải bất phương trình.
- Cách giải:
+ Ta có: 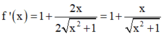
+ Theo đề bài ta có: 2x.f'(x) - f(x) ≥ 0.
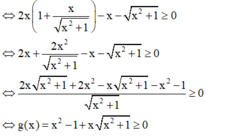
+ Thử các đáp án:
+ Với 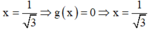 thuộc tập nghiệm của BPT.
thuộc tập nghiệm của BPT.
⇒ Loại đáp án A, B và C.
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
Cho hàm số y = f(x) có f'(x)>0 ∀ x ∈ ℝ . Tìm tập hợp tất cả các giá trị thực của x để f 1 x < f ( 1 )
![]()
![]()
![]()
![]()
Cho hàm số \(y=f\left(x\right)\) liên tục trên R, có đạo hàm \(f'\left(x\right)=x\left(x-1\right)^2\left(x-2\right)\) . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho hàm số \(y=f\left(\dfrac{x+2}{x+m}\right)\) đồng biến trên khoảng \(\left(10;+\infty\right)\) . Tính tổng các phần tử của S.
Cho hàm số y=f(x) có f'(x)>0 với mọi x. Tìm tập hợp tất cả các giá trị thực của x để f 1 x < f(1)
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hàm số ![]() có
có ![]() thì đồng biến trên R.
thì đồng biến trên R.
Khi đó ta có
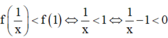
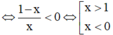
Vậy ![]()
Chọn B