\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)

a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)

Với \(x = 2\) thì \(y = {\log _2}2 = 1\)

Với \(x = 4\) thì \(y = {\log _2}4 = 2\)

b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.

Đáp án B

Ta có log(x + 2y) = log x + log y

<=> log 2 (x+2y) = log 2xy

<=> 2 (x+2y) = 2xy (*).

Đ ặ t   a = x > 0 b = 2 y > 0 , khi đó

* ⇔ 2 a + b = a b

và  P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2

Lại có  a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8 .

Đặt t = a + b, do đó

P ≥ f t = t 2 t + 2 .

X é t   h à m   s ố   f t = t 2 t + 2 t r ê n   [ 8 ; + ∞ )

c ó   f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ ≥ 8

Suy ra f(t) là hàm số đồng biến trên  [ 8 ; + ∞ )

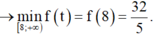
Vậy gía trị nhỏ nhất của biểu thức P là  32 5 .

a) \(log_69+log_64=log_636=2\)

b) \(log_52-log_550=log_5\left(2:50\right)=-2\)

c) \(log_3\sqrt{5}-\dfrac{1}{2}log_550=-1,0479\)

Đáp án C

\(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}=\dfrac{a^2\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{4}{5}}}{a^{\dfrac{1}{4}}}=\dfrac{a^{\dfrac{47}{15}}}{a^{\dfrac{1}{4}}}=a^{\dfrac{173}{60}}\)

\(\Rightarrow log_a\left(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}\right)=log_a\left(a^{\dfrac{173}{60}}\right)=\dfrac{173}{60}\)

\(a^{2log_a\left(\dfrac{\sqrt{105}}{30}\right)}=a^{log_a\left(\dfrac{7}{60}\right)}=\dfrac{7}{60}\)

Vậy \(B=\dfrac{173}{60}+\dfrac{7}{60}=\dfrac{180}{60}=3\)

a) \(log_29\cdot log_34=4\)

b) \(log_{25}\cdot\dfrac{1}{\sqrt{5}}=-\dfrac{1}{4}\)

c) \(log_23\cdot log_9\sqrt{5}\cdot log_54=\dfrac{1}{2}\)

\(4^{\log_23}=\left(2^2\right)^{\log_23}=2^{2log_23}=2^{\log_23^2}=2^{\log_29}=9\)

-> A

Chọn A

a: \(log_{\dfrac{1}{4}}8=log_{2^{-2}}2^3=\dfrac{-3}{2}\cdot log_22=-\dfrac{3}{2}\)

b: \(log_45\cdot log_56\cdot log_68\)

\(=log_45\cdot\dfrac{log_46}{log_45}\cdot\dfrac{log_48}{log_46}\)

\(=log_48=log_{2^2}2^3=\dfrac{3}{2}\)

Đáp án A.