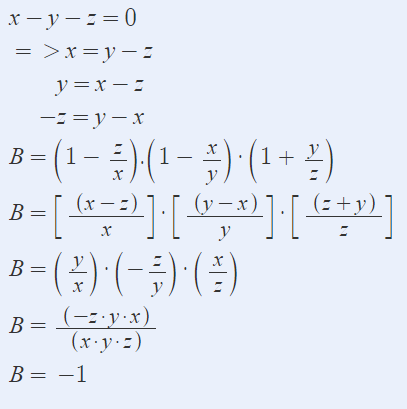Cho x.y.z=2 và x+y+z=0
Tính giá trị biểu thức: Q= ( x+y).(y+z).(x+z)

Những câu hỏi liên quan
Cho x,y,z ko bằng 0 và x-y-z=0
Tính giá trị biểu thức: B= (1-z/x).)(1-x/y).(1+y/z)+2023
x-y-z=0
=>x=y+z và y=x-z và z=x-y
B=(1-z/x)(1-x/y)(1+y/z)+2023
\(=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{y+z}{z}+2023\)
\(=\dfrac{y}{x}\cdot\dfrac{-z}{y}\cdot\dfrac{x}{z}+2023=2023-1=2022\)
Đúng 0
Bình luận (0)
cho x.y.z=2 và x+y+z=0.tính giá trị của biểu thức M=(x+y)(y+z)(z+x)
cho x,y,z khác 0 và x-y-z = 0
Tính giá trị biểu thức B= \(\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
Cho x.y.z=2 và x+y+z=0. Tính giá trị biểu thức sau:
C= (x+y).(y+z).(x+z)
Ta có x+y+z = 0
\(\Rightarrow\left(+\right)x+y=-z\)
\(\left(+\right)x+z=-y\)
\(\left(+\right)z+y=-x\)
C= (x+y)(y+z)(x+z)=(-z)(-x)(-y)=-1(xyz)=-1. 2= -2
Đúng 0
Bình luận (0)
tính giá trị của biểu thức:
(x+y).(y+z).(z+x)biết x+y+z=0 và x.y.z=2000
\(x+y+z=0\Rightarrow\hept{\begin{cases}x+y=-z\\x+z=-y\\y+z=-x\end{cases}}\)
\(\Rightarrow\left(x+y\right)\left(y+z\right)\left(x+z\right)=-xyz=-2000\)
~~
cho x, y, z thỏa mãn hệ phương trình
\(\hept{\begin{cases}x^2+y^2+z^2=1\\x^3+y^3+z^3=1\end{cases}}\)
Tính giá trị biểu thức P=x.y.z
Ta có \(x^2+y^2+z^2=1\) \(\Rightarrow\hept{\begin{cases}x^2\le1\\y^2\le1\\z^2\le1\end{cases}}\)
\(\Rightarrow-1\le x,y,z\le1\) (*)
Lấy pt sau trừ pt trước ta được \(x^2\left(x-1\right)+y^2\left(y-1\right)+z^2\left(z-1\right)=0\)
Mà từ (*) ta suy ra \(\hept{\begin{cases}x^2\left(x-1\right)\ge0\\y^2\left(y-1\right)\ge0\\z^2\left(z-1\right)\ge0\end{cases}}\)
Do vậy dấu "=" chỉ xảy ra khi \(x^2\left(x-1\right)=y^2\left(y-1\right)=z^2\left(z-1\right)=0\)
Xảy ra 4 trường hợp :
+ TH1 : Nếu x = y = z = 0 => \(x^2+y^2+z^2=x^3+y^3+z^3=0\ne1\)không thỏa mãn - loại
+ TH2 : Nếu \(x=y=z=1\)=> \(x^2+y^2+z^2=x^3+y^3+z^3=3\ne1\)không thỏa mãn - loại
+ TH3 : Nếu hai trong bộ ba số (x;y;z) nhận giá trị là 1 và số còn lại nhận giá trị bằng 0 thì \(x^2+y^2+z^2=x^3+y^3+z^3=2\ne1\) không thỏa mãn - loại
+ TH4 : Nếu hai trong bộ ba số (x;y;z) nhận giá trị là 0 và số còn lại nhận giá trị bằng 1 thì :
\(x^2+y^2+z^2=x^3+y^3+z^3=1\) thỏa mãn - nhận
Do trong ba số này vai trò của x,y,z là bình đẳng nên ta có thể chọn x = y = 0 , z = 1
=> xyz = 0 => P = 0
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức;
C=(x+y)(y+z)(x+z)
Khi x+y+z=0va x.y.z=-2017
Từ x+y+z=0
=>x+y=-z
x+z=-y
y+z=-x
thay vào C,ta có:C=(x+y)(y+z)(x+z)
=(-z)(-x)(-y)
Vì x.y.z=-2017
=>(-z)(-x)(-y)=2017
Vậy C=(x+y)(y+z)(x+z)=2017
Đúng 0
Bình luận (0)
a) Cho x,y,z khác 0 và x-y-z = 0. Tính giá trị biểu thức A = \(\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\)b) Cho x,y,z thoả mãn x.y.z = 1. Chứng minh \(\frac{1}{xy+x+1}+\frac{y}{yz+y+1}+\frac{1}{xyz+yz+y}=1\)
\(A=\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\)
\(A=\frac{x-z}{x}\cdot\frac{y-x}{y}\cdot\frac{y+z}{z}\)
Do \(x-y-z=0\)
\(\Rightarrow x-z=y;y-x=-z;y+z=x\)
Khi đó \(A=\frac{y}{x}\cdot\frac{-z}{y}\cdot\frac{x}{z}=-1\)
Vậy A=-1
Đúng 0
Bình luận (0)
\(\frac{1}{xy+x+1}+\frac{y}{yz+y+1}+\frac{1}{xyz+yz+y}\)
\(=\frac{1}{xy+x+1}+\frac{y}{yz+y+1}+\frac{1}{1+yz+y}\)
\(=\frac{1}{xy+x+1}+\frac{y+1}{yz+y+1}\)
\(=\frac{yz}{xy\cdot yz+xyz+yz}+\frac{y+1}{yz+y+1}\)
\(=\frac{yz}{yz+y+1}+\frac{y+1}{yz+y+1}\)
\(=\frac{yz+y+1}{yz+y+1}\)
\(=1\)
Đúng 0
Bình luận (0)
Tính giá trị của đa thức B= (x + y).(y + z).(z + x) với x + y +z=0 và x.y.z= -2016
x+y+z=o suy ra x+y=-z ;z+x=-y;z+y=-x
B=-z.-x.-y=-xyz=-(-2016)=2016
Đúng 0
Bình luận (0)
Từ giả thiết x + y + z = 0 => x + y = - z; y + z = -x và x + z = -y
Vậy B = (x + y)(y + z) (z + x) = -z.(-x).(-y) = - xyz = 2016
Vậy B = 2016