\(chứng minh rằng tam giác cân có 1 góc bằng 60 độ là tam giác đều.\)

Những câu hỏi liên quan
chứng minh rằng:
- trong tam giác đều 3 góc bằng nhau và bằng 60 độ
- 1 tam giác có 2 góc bằng nhau và bằng 60 độ là tam giác đều
- tam giác cân có 1 góc bằng 60 độ là tam giác đều
2) góc còn lại là 180 - 2.60=60
vậy 3 góc =60 độ => tam giác đều
Đúng 0
Bình luận (0)
1) 3 góc = nhau => 3*A=180 độ (gọi 3 góc là A,B,C)
=> a=60 độ = góc B = góc C
Đúng 0
Bình luận (0)
giả sử tam giác ABC cân tại A => B=C=60 độ => góc A = 180 -60-60=60=> tam giác đều
với tam giác cân tại B và C thì CMTT
Đúng 0
Bình luận (0)
Nếu một tam giác cân có một một góc bằng 60 độ thì tam giác ấy là tam giác đều ? Chứng minh.
Cái này có trong định lí hay dấu hiệu nhận biết rồi :v
Đúng 0
Bình luận (0)
Nếu một tam giác cân có một một góc bằng 60 độ thì tam giác ấy là tam giác đều ? Đúng r
Các cách chứng minh tam giác đều gồm, tham khảo:
– Cách 1: Chứng minh tam giác đó có 3 cạnh bằng nhau.
– Cách 2: Chứng minh tam giác đó có 3 góc bằng nhau.
– Cách 3: Chứng minh tam giác đó cân và có một góc bằng 60 độ.
– Cách 4: Chứng minh tam giác đó có 2 góc bằng 60 độ.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều.
Nếu góc bằng 60 độ là góc ở đáy => Góc đáy bên còn lại cũng bằng 60 độ (tam giác cân)
=> Góc ở đỉnh là 180 - 60 - 60 = 60 độ
Nếu góc ở đỉnh là 60 độ => Tổng 2 góc đáy bằng 180 - 60 = 120 độ
Mà 2 góc đáy bằng nhau (tam giác cân) nên chúng cùng bằng 120 : 2 = 60 độ
Ở cả 2 trường hợp thì tam giác đều có 3 góc bằng 60 độ => Đó là tam giác đều
Chúc bạn học tốt!
Bài 1: Trong các câu sau, câu nào đúng, câu nào sai?
A. Tam giác có hai góc bằng 60 độ là tam giác đều
B. Tam giác có hai cạnh bằng nhau và một góc bằng 60 độ là tam giác đều
C. Tam giác cân có một góc bằng 45 độ là tam giác vuông cân
D. Tam giác có hai góc bằng 45 độ là tam giác vuông cân
1) chứng minh định lý: nếu một tam giác có hai góc ở đấy bằng nhau thì tam giác đó là tam giác cân
2) chứng minh định lý: nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều
Cho tam giác ABC cân tại A có góc B bằng \({60^o}\). Chứng minh rằng tam giác ABC đều.
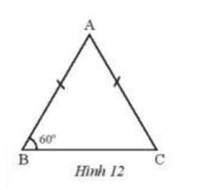
Ta có: tam giác ABC cân tại A
Nên \(\widehat B = \widehat C = {60^o}\)( 2 góc đáy của tam giác cân )
Theo định lí về tổng 3 góc trong tam giác ta có : \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat A = {180^o} - {60^o} - {60^o} = {60^o}\)
Vì \(\widehat A = \widehat B = \widehat C = {60^o}\)\( \Rightarrow \) tam giác ABC là tam giác đều
Đúng 0
Bình luận (0)
1.Cho tam giác ABC cân đỉnh A, góc BAx là góc ngoài tại đỉnh A của tam giác ABC. Chứng minh rằng góc BAx bằng 2.B
2.Cho tam giác ABC có góc A bằng 90, góc B bằng 60. Chứng minh rằng AB = 1/2 BC.
cho hình vuông ABCD. Điểm E nằm trong hình vuông sao cho tam giác ECD cân có góc đấy bằng 15 độ. Chứng minh rằng tam giác ABE là tam giác đều
Cho tam giác ABC đều , chứng minh rằng các góc của tam giác đều bằng 60 độ
\(\Delta ABC.deu\Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=\frac{180^o}{3}=60^o\) (do tong so do 3 goc cua 1 tam giac =180 o )
Study well
Đúng 0
Bình luận (0)
Tam giác ABC đều
\(\Rightarrow\widehat{A}=\widebat{B}=\widehat{C}\)
Mà \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=\frac{180}{3}=60^0\)
Đúng 0
Bình luận (0)
























