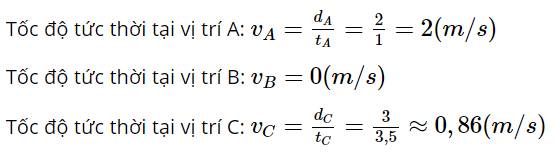Hình 4.11 có A B ⊥ A C , C D ⊥ A C và O E ⊥ A C . Biết O A B ^ = m ° ; O C D ^ = 50 ° . Tìm giá trị m để tia OE là tia phân giác của góc AOC

Những câu hỏi liên quan
Một vật chuyển động thẳng có đồ thị (d – t) được mô tả như Hình 4.11. Hãy xác định tốc độ tức thời của vật tại các vị trí A, B và C.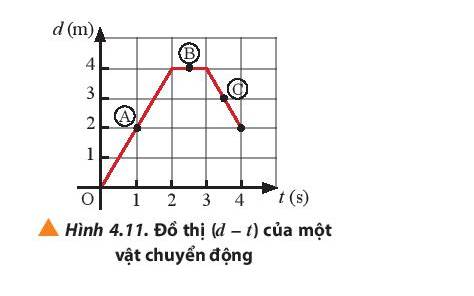
Một vật chuyển động thẳng có đồ thị (d – t) được mô tả như Hình 4.11. Hãy xác định tốc độ tức thời của vật tại các vị trí A, B và C.
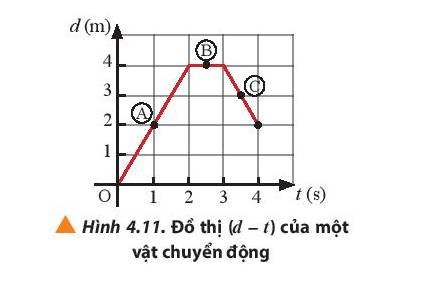
Tốc độ tức thời tại vị trí A: \({v_A} = \frac{{{d_A}}}{{{t_A}}} = \frac{2}{1} = 2(m/s)\)
Tốc độ tức thời tại vị trí B: \({v_B} = 0(m/s)\)
Tốc độ tức thời tại vị trí C: \({v_C} = \frac{{{d_C}}}{{{t_C}}} = \frac{3}{{3,5}} \approx 0,86(m/s)\)
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O’) cắt nhau ở A và B. Kẻ tiếp tuyến chung CD của hai đường tròn, C∈ (O); D ∈ (O’). Gọi I là giao điểm của AB và CD. Gọi E là điểm đối xứng với B qua I. Chứng minh rằng: a) BCED là hình bình hành b) Bốn điểm A, C, E , D thuộc cùng một đường tròn
cho 4 điểm A,B,C,D trong đó có 3 điểm A,B,C thẳng hàng.B,C,D thảng hàng
a,4 điểm A,B,C,D có thẳng hàng không vì sao
b,E là điểm không thuộc đường thẳngAB.Nối E với A,B,C,D.Kể tên các đoạn thẳng và các hình tam giác vẽ
Cho hình thang ABCD có góc A = góc D = 90¤ . Hai đường chéo AC và BD vuông góc với nhau tại i.
a/ c/m tam giác ABD ~ tam giác DAC => AD2 = AB.DC
b/ gọi e là hình chiếu của B xuống DC và O là trung điểm BD
c/. c/m : 3 điểm A,O,E thẳng hàng c/ tính tỉ số diệm tích tam giác AIB và DIC
Cho $\widehat{xOy}$. Lấy các điểm $A, \, B$ thuộc tia $O x$ sao cho $O A>O B$. Lấy các điểm $C, \, D$ thuộc $O y$ sao cho $O C=O A, \, O D=O B$. Gọi $E$ là giao điểm của $A D$ và $B C$. Chứng minh rằng
a) $A D=B C$.
b) $\triangle A B E=\triangle C D E$.
c) $O E$ là tia phân giác của $\widehat{x O y}$.
a)
Xét \(\Delta AOD\) và \(\Delta COB\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}:chung\\OB=OD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\)
\(\Rightarrow AD=BC\left(\text{2 cạnh tương ứng}\right)\left(\text{đpcm}\right)\)
b)
Nối A với C
Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=OD\end{matrix}\right.\left(gt\right)\Rightarrow OA-OB=OC-OD\)
Hay \(AB=CD\)
Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\left\{{}\begin{matrix}AB=CD\left(cmt\right)\\AC:chung\\AD=BC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DCA\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{CDA}\left(\text{2 góc tương ứng}\right)\)
Vì \(\Delta AOD=\Delta COB\left(cmt\right)\Rightarrow\widehat{A}=\widehat{C}\left(\text{2 góc tương ứng}\right)\)
Xét \(\Delta ABE\) và \(\Delta CDE\) có: \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{CDA}\left(cmt\right)\\AB=CD\left(cmt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\left(\text{đpcm}\right)\)
c) Vì \(\Delta ABE=\Delta CDE\left(cmt\right)\Rightarrow AE=CE\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta AOE\) và \(\Delta COE\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\\AE=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOE=\Delta COE\left(c.g.c\right)\\ \Rightarrow\widehat{AOE}=\widehat{COE}\left(\text{2 góc tương ứng}\right)\)
`=> OE` là phân giác của \(\widehat{xOy}\) (đpcm)
Đúng 2
Bình luận (1)
a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
COE
(hai góc tương ứng)
là tia phân giác của .
Đúng 0
Bình luận (0)
a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho các điểm A,B,C,D,E trong đó A,B,C cung thuộc đường thẳng a;C,D,E cung thuộcđường thẳng b và B,C,D là ba điểm ko thẳng hàng
a,vẽ hình
b,3 điểm A,B,D có là 3 điểm thẳng hàng ko? tại sao?
bài 5 :
a,vẽ bốn điểm A,B,C,D sao cho A,b,C thẳng hàng và B,C,D thẳng hàng . hỏi bốn điểm A,B ,C,D có luôn luôn thẳng hàng hay không ?
b,vẽ năm điểm A,B,C,D ,E sao cho A,b,C thẳng hàng và B,E ,D thẳng hàng . hỏi năm điểm A,B ,C,D,E có luôn luôn thẳng hàng hay không ?
a: Bốn điểm A,B,C,D luôn thẳng hàng
b: 5 điểm A,B,C,D,E có thể không thẳng hàng
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi
V
1
là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′,
V
2
là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích
V
1
V
2...
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi V 1 là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′, V 2 là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích V 1 V 2 là
A. 6
B. 2
C. 8
D. 4
Cho tam giác $A B C$ nhọn nội tiếp đường tròn $(O, R)$. Các đường cao $A D, B E, C F$ cắt nhau tại $H$. Kẻ đường kính $A G$. Gọi $I$ là trung điểm $B C$.
a) Chứng minh 4 điểm $B, C, E, F$ cùng nằm trên 1 đường tròn.
b) Chứng minh $D H . D AD B . D C$ và tứ giác $B H C G$ là hình bình hành.
c) Cho $B C$ cố định, điểm $A$ chuyển động trên cung lớn $B C$ sao cho tam giác $A B C$ nhọn. Tìm vi trí của $A$ để diện tích $Delta A E H$ lớn nhất.
Đọc tiếp
Cho tam giác $A B C$ nhọn nội tiếp đường tròn $(O, R)$. Các đường cao $A D, B E, C F$ cắt nhau tại $H$. Kẻ đường kính $A G$. Gọi $I$ là trung điểm $B C$.
a) Chứng minh 4 điểm $B, C, E, F$ cùng nằm trên 1 đường tròn.
b) Chứng minh $D H . D A=D B . D C$ và tứ giác $B H C G$ là hình bình hành.
c) Cho $B C$ cố định, điểm $A$ chuyển động trên cung lớn $B C$ sao cho tam giác $A B C$ nhọn. Tìm vi trí của $A$ để diện tích $\Delta A E H$ lớn nhất.
Vì BE vuông góc với AC tại E (E ϵAC) ⇒ góc BEC =\(90^0\)
Vì CF vuông góc với AB tại F (F ϵ AB) ⇒ góc BFC =\(90^0\)
xét tứ giác BCEF có ;
góc BEC+BFC=\(90^0+90^0=180^0\)
mà hai góc ở vị trí kề nhau
⇒tứ giác BCEF là tgnt hay A,C,E,F cùng nằm trên một đtròn
b,