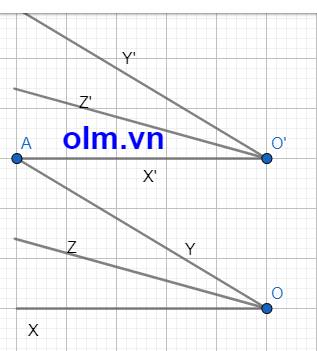
a,Kéo dài OY cắt O'X' tại A ta có: 

  \(\widehat{XOY}\) =  \(\widehat{XOA}\)  = \(\widehat{OAO'}\) (so le trong) (1)

   \(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)

Kết hợp (1) Và (2) ta có:

    \(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)

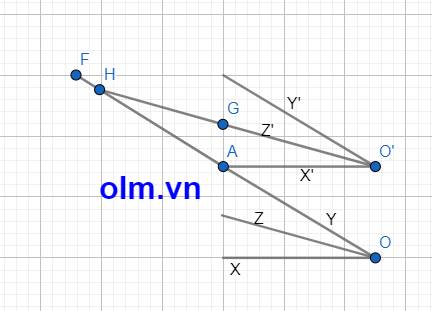
b, Kéo dài OY cắt O'Z' tại H 

             \(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY

             \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')

         Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

               \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\)  ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)

          ⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)

         ⇒ OZ // O'Z' (đpcm)

hình bên đâu bẹn???

ai giúp mik vs mik cần gấp

cho mik cái hình đã

Các góc nhọn là góc xOm, góc yOn

Góc vuông: góc mOn

Góc tù: góc xOn, góc yOm

1)   TA CÓ xOy +yOz =180*

xOy +x'Oy =180* 

=>yOz =x'Oy 

=>Oy tia phân giác x'Oy

Số góc 12 tia chung gốc  tạo thành là:

   \(\dfrac{n.\left(n-1\right)}{2}=\dfrac{12.\left(12-1\right)}{2}=66\) ( góc )

 Vậy có 66 góc được tạo bởi 12 tia chung gốc.

a) góc zOx

góc yOz

góc xOy

b)ta có \(\widehat{yOt}=\widehat{zOy}+\widehat{zOt}>\widehat{zOy}\)

9 góc đỉnh O

9 góc đỉnh O 

9