Khoảng cách giữa hai đường thẳng d 1 : a x + b y + c = 0 v à d 2 : a x + b y + d = 0 được cho bởi công thức nào sau đây?
A. c − d a 2 + b 2
B. c + d a 2 + b 2
C. c − d a 2 + b 2
D. c + d a 2 + b 2
a) Tính khoảng cách từ điểm \(O\left( {0{\rm{;}}0} \right)\) đến đường thẳng \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1\)
b) Tính khoảng cách giữa hai đường thẳng song song \({\Delta _1}:x - y + 1 = 0\)và \({\Delta _2}:x - y - 1 = 0\)
a) Ta có: \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1 \Leftrightarrow x - 2y + 4 = 0\)
Vậy khoảng cách từ O đến \(\Delta \) là: \(d\left( {O;\Delta } \right) = \frac{{\left| {1.0 - 2.0 + 4} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \frac{{4\sqrt 5 }}{5}\)
b) Lấy \(M\left( {0;1} \right) \in {\Delta _1}\)
Suy ra: \(d\left( {{\Delta _1},{\Delta _2}} \right) = d\left( {M,{\Delta _2}} \right) = \frac{{\left| {0 - 1 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 \)
Cho hai đường thẳng (d): 2x-y-2=0 và (d’): 4x-2y+6=0.Khoảng cách giữa hai đường thẳng là:
\(A,-\sqrt{5}\)
\(B,2\sqrt{5}\)
\(C\sqrt{5}\)
D.5
NX: \(\dfrac{2}{4}\)=\(\dfrac{-1}{-2}\)≠\(\dfrac{-2}{6}\)
=> (d) // (d')
Ta lấy điểm A(0;-2) ∈ d
d(d;d') = \(\dfrac{\left|4.0-2.\left(-2\right)+6\right|}{\sqrt{4^2+2^2}}\) = \(\sqrt{5}\)
=> Chọn C
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Cho hàm số y= 2x3-3x2+1 có đồ thị và đường thẳng d: y=x-1. Giao điểm của (C) và d lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C là
A. BC= 30 2
B. BC= 34 2
C. BC= 3 2 2
D. BC= 14 2
2x3-3x2+1 =x-1 hay 2x3-3x2-x+2=0
![]()
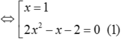
Khi đó ta có A(1 ; 0) ; B( x1 ; x1-1) và C( x2 ; x2-1) ( x1 ; x2 là nghiệm của (1))
Ta có ![]() , suy ra
, suy ra
![]()
![]()
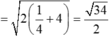
Chọn B.
Cho hàm số y = 2 x − 1 x + 1 có đồ thì (C) và đường thẳng d : y = 2 x − 3. Đường thẳng d cắt (C) tại hai điểm A và B. Khoảng cách giữa A và B là
A. A B = 2 5 5
B. A B = 5 2
C. A B = 5 5 2
D. A B = 2 5
Đáp án C
Phương trình hoành độ giao điểm 2 x − 1 x+ 1 = 2 x − 3 ⇔ 2 x 2 − 3 x − 2 = 0 ⇔ x = 2 x = − 1 2
Vậy A ( 2 ; 1 ) ; B ( − 1 2 ; − 4 )
AB → = − 1 2 − 2 2 + − 4 − 1 2 = 5 5 2
Đường thẳng d: y = x - 5 cắt đồ thị (C): y = x + 1 x - 3 tại hai điểm A, B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng ∆ : x = 0 . Tính d = d 1 + d 2
A. d = 9
B. d = -1
C. d = 5
D. d = 5 2
Đáp án C
Phương trình hoành độ giao điểm : x + 1 x - 3 = x - 5 ⇔ x ≠ 3 x 2 - 9 x + 14 = 0 ⇔ x = 7 ⇒ y = 2 x = 2 y ⇒ = - 3
Do đó A 7 ; 2 ; B 2 ; - 3 ⇒ d = d 1 + d 2 = 2 + 3 = 5 .
Cho đường thẳng d : -3x+y-1=0 và điểm I(-2;4).
a. Viết pt đường thẳng d1 đối xứng với đường thẳng d2 : 2x+y=0 qua d
b. Viết pt đường thẳng d3 sao cho khoảng cách giữa d và d3 bằng 6
Đường thẳng d : y = x - 3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng D: x-y=0. Tính d = d 1 + d 2
A. d = 3 2
B. d = 3 2 2
C. d = 6
D. d = 2 2