Nếu ba vecto a → , b → , c → cùng vuông góc với vecto n → khác 0 → thì chúng.
A. đồng phẳng
B. không đồng phẳng
C. có thể đồng phẳng
D. có thể không đồng phẳng
Những câu hỏi liên quan
Cho ba vecto
n
→
,
a
→
,
b
→
bất kì đều khác với vecto
0
→
. Nếu vecto
n
→
vuông góc với cả hai vecto
a
→
v
à
b
→
thì
n
→
,
a
→
v
à...
Đọc tiếp
Cho ba vecto n → , a → , b → bất kì đều khác với vecto 0 → . Nếu vecto n → vuông góc với cả hai vecto a → v à b → thì n → , a → v à b → :
A. đồng phẳng
B. không đồng phẳng
C. có giá vuông góc với nhau từng đôi một
D. có thể đồng phẳng
Phương án A sai vì có thể xảy ra trường hợp giống câu 4 như hình sau:
Phương án B và C sai vì có thể sảy ra như hình sau.
Phương án D đúng vì: có thể ba vecto n → , a → , b → đồng phẳng hoặc không đồng phẳng như hai hình trên.
Đáp án D
Đúng 0
Bình luận (0)
Cho vecto
n
→
≠
0
→
và hai vecto
a
→
v
à
b
→
không cùng phương. Nếu vecto
n
→
vuông góc với cả hai vecto
a
→
v
à
b
→
thì
n
→
,
a
→...
Đọc tiếp
Cho vecto n → ≠ 0 → và hai vecto a → v à b → không cùng phương. Nếu vecto n → vuông góc với cả hai vecto a → v à b → thì n → , a → v à b → :
A. đồng phẳng
B. không đồng phẳng
C. có thể đồng phẳng
D. có thể không đồng phẳng
Phương án A và C sai vì có thể xảy ra trường hợp như hình vẽ sau
Giả sử phương án B cũng sai, tức là ba vecto n → , a → v à b → đồng phẳng. Khi đó vì n→ ⊥ a→ và n→ ⊥ b→ nên giá của a → v à b → song song. Điều này mẫu thuẫn với giả thiết hai vecto a → v à b → không cùng phương. Vì vậy phương án B đúng.
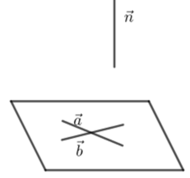
Đáp án B
Đúng 0
Bình luận (0)
cho vectơ u=vectơ a +3 vecto b vuông góc với vectơ v=7 vecto a-5 vecto b và vecto x= vecto a-4 vecto b vuông góc với vecto y=7 vecto a-2 vecto b. khi đó góc giữa 2 vecto a và b bằng bao nhiêu
Cho hai vectơ
a
→
và
b
→
khác vecto không và thảo mãn
u
→
a
→
+
b
→
vuông góc với vecto
v
→
2
a
→
-
3
b
→
và
m...
Đọc tiếp
Cho hai vectơ a → và b → khác vecto không và thảo mãn u → = a → + b → vuông góc với vecto v → = 2 a → - 3 b → và m → = 5 a → - 3 b → vuông góc với n → = - 2 a → + 7 b → . Tính góc tạo bởi hai vecto a → và b →
A. 60 °
B. 45 °
C. 90 °
D. 30 °
Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương hay không?
b) Ngược lại, nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.
Đúng 0
Bình luận (0)
Cho 2 vecto a và b có giá vuông góc với nhau và |vecto a|=5;|vecto b|=12.Tính |vecto a-vecto b| và |vecto a+vecto b|
giúp mk với ạ
Cho tam giác ABC vuông tại A có AB=3 góc B=60° .Gọi M là điểm thỏa vecto MA + vecto MB= vecto 0. Tính độ dài vecto BM + vecto BC + vecto BA
Cho 2 vecto : vecto u = 2. vecto a + vecto b và vecto v = vecto a - 3 vecto b . Hai vecto này vuông góc với nhau. Biết vecto a = căn 2, vecto b = căn 3. Chứng minh vecto a . Vecto b = -1
Xem chi tiết
30 tháng 11 2023 lúc 23:09
Cho tứ giác ABCD. Chứng minh rằng nếu |vecto AD + vecto BC| = |vecto AB + vecto DC| thì AC vuông góc với BD