Cho hàm số y = x 3 − 2 x + 1 có đồ thị (C). Hệ số góc của tiếp tuyến với (C) tại điểm M(-1;2) bằng
A. 1
B. -5
C. 25
D. 3
Cho hàm số \(y = {x^3} - 3{x^2} + 4x - 1\) có đồ thị là \((C)\). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm \(M\) trên đồ thị \((C)\) là
A. 1 .
B. 2.
C. -1 .
D. 3 .
\(y'=\left(x^3-3x^2+4x-1\right)'=3x^2-3\cdot2x+4\)
\(=3x^2-6x+3+1=3\left(x-1\right)^2+1>=1\)
Dấu = xảy ra khi x=1
=>Chọn A
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
Cho hàm số \(y = {x^3} - 3{{\rm{x}}^2}\). Tiếp tuyến với đồ thị của hàm số tại điểm \(M\left( { - 1;4} \right)\) có hệ số góc bằng:
A. ‒3.
B. 9.
C. ‒9.
D. 72.
Ta có: \(y'3x^2-3.2x=3x^2-6x\).
Tiếp tuyến với đồ thị của hàm số tại điểm \(M\left(-1;4\right)\) có hệ số góc bằng:\(y'\left(-1\right)=3.\left(-1\right)^2-6.\left(-1\right)=9\).
\(\Rightarrow B\)
Đề bài
Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)
a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)
Cho hàm số y = x 4 + x 2 − 3 có đồ thị (C). Khi đó hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = 1 là
A. -1
B. 2
C. -4
D. 6
Cho hàm số y = x 4 + x 2 − 3 có đồ thị (C). Khi đó hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = 1 là
A. -1.
B. 2.
C. -4.
D. 6.
Cho hàm số y = 2 x + 1 2 x - 1 có đồ thị (C). Hệ số góc của tiếp tuyến với (C) tại điểm M(0;-1) bằng
A.4
B.1
C.0
D.-4
Cho hàm số y = 2 x + 1 2 x - 1 có đồ thị (C). Hệ số góc của tiếp tuyến với (C) tại điểm M(0;-1) bằng
A. 4.
B. 1.
C. 0.
D. -4.
Chọn D.
Tập xác định: 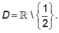
Ta có 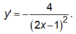
Hệ số góc của tiếp tuyến với (C) tại điểm M(0;-1) là y'(0) = -4
Cho hàm số y=\(x^3-3x^2-1\)có đồ thị (C).Điểm M(a;b) trên(C) có hoành độ thuộc [2;3] sao cho tiếp tuyến của (C) tại M có hệ số góc lớn nhất.Khi đó, S=a+b=?
\(y'=3x^2-6x\)
Do M thuộc (C) nên hệ số góc của tiếp tuyến tại M:
\(k=f\left(a\right)=3a^2-6a\)
\(f'\left(a\right)=6a-6>0;\forall a\in\left[2;3\right]\)
\(\Rightarrow f\left(a\right)\) đồng biến trên \(\left[2;3\right]\Rightarrow k_{max}\) khi \(a=3\)
\(\Rightarrow b=a^3-3a^2-1=-1\)
\(S=3-1=2\)