Điểm nằm trên đường tròn C : x 2 + y 2 - 2 x + 4 y + 1 = 0 có khoảng cách ngắn nhất đến đường thẳng d:x-y+3=0 có tọa độ M(a;b). Khẳng định nào sau đây là đúng?
A. 2 a = - b .
B.a=-b
C. 2 a = b .
D.a=b
Trong mặt phẳng toạ độ Oxy, nêu mối liên hệ giữa x và y để:
a) Điểm M(x ; y) nằm trên đường tròn tâm O(0 : 0) bán kính 5.
b) Điểm M(x ; y) nằm trên đường tròn (C) tâm I(a; b) bán kính R.
a) Mối liên hệ giữa x và y là: \({x^2} + {y^2} = 5\)
b) Mối liên hệ giữa x và y là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)
Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn tâm O bán kính bằng 1 và nằm trên đường thẳng Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn tâm O bán kính bằng 1 và nằm trên đường thẳng x + y = 2
![]()
![]()
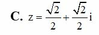
![]()
trong mặt phẳng tọa độ Oxy cho điểm E(3;4), đường thẳng d : x + y - 1 = 0 và đường tròn (C) : x2 + y2 + 4x - 2y - 4 = 0 . Gọi M (m;1-m) là điểm nằm trên đường thẳng d và nằm ngoài đường tròn (C), từ M kẻ các tiếp tuyến MA, MB tới đường tròn (C), với A,B là các tiếp điểm. Gọi (E) là đường tròn tâm E và tiếp xúc với đường thẳng AB. Khi đường tròn (E) có chu vi lớn nhất. Tìm tọa độ điểm M
(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)
Cho đường tròn ( O ; R ) đường kính AB . Vẽ tiếp tuyến x , y qua A . Trên xy lấy điểm C khá A . Đoạn thẳng BC cắt (O) tại D . Gọi E là trung điểm của DB, i là trung điểm của AC . Chứng mình :
a, BD.BC = \(4R^2\)
b, Bốn điểm A , C , E , O cùng nằm trên một đường tròn .
c, DI là tiếp tuyến của đường tròn (O)
d, Khi điểm C di chuyển trên x,y thì điểm E chạy trên đường nào ? Vì sao ?
Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn tâm O bán kính bằng 1 và nằm trên đường thẳng x + y = 2
A. z = 2 i
B. z = 2 2 + 2 2 i
C. z = 2 − 1 + i
D. z = 2
Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn tâm O bán kính bằng 1 và nằm trên đường thẳng x + y = 2
A. z = 2 - 1 + i
B. z = 2 i
C. z = 2 2 + 2 2 i
D. z = 2
Đáp án C
Tọa độ điểm biểu diễn s phức z thỏa mãn hệ phương trình
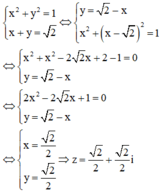
Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn tâm O bán kính bằng 1 và nằm trên đường thẳng x + y = 2
![]()
![]()
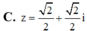
![]()
Đáp án D
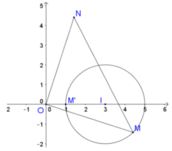
Gọi z 1 = x + y i ; x , y ∈ ℝ .
Khi đó điểm biểu diễn số phức z 1 là M(x;y) thỏa mãn.
Do đó tập hợp các điểm biểu diễn số phức z 1
là đường tròn tâm I(3;0) bán kính R = 2
Ta có z 2 = i z 1 = i x + y i = - y + i x .
Khi đó tam giác MON vuông cân tại O.
M N = O M 2 nên MN nhỏ nhất
Û OM nhỏ nhất
Û M ≡ M ' (M’ là giao điểm của OI với đường tròn
về phía bên trái như hình vẽ).
Tức là M(1;0). Khi đó M N = 2 O M = 2 . 1 = 2
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \(x^2+y^2-2x-2y+1=0\) và đường thẳng \(d=x-y+3=0\). Tìm tọa độ điểm M nằm trên d sao cho đường tròn tâm M có bán kính gấp đôi bán kính đường tròn (C) và tiếp xúc ngoài với đường tròn (C)
Cho đường tròn (O;R) lấy điểm A nằm trên đường tròn và điểm H nằm trong đường tròn đó, sao cho AH=Rcăn2. Xác định hai điểm B, C nằm trên đường tròn sao cho H là trực tâm tam giác ABC. Khi đó chứng minh rằng AB^2+AC^2-AB.AC.căn2=2R^2
viết pt đường tròn qua 2 điểm A(0;1) B(2;-2) và tâm nằm trên đường thẳng (d) x-y-2=0
gọi I là tâm dường tròn => d(A,d)=IA=R
tọa độ I là (x,y)
=> R= d(A,d)= \(\frac{3}{\sqrt{2}}\)
=> \(\left|\overrightarrow{IA}\right|=\sqrt{x^2+\left(1-y\right)^2}=\frac{3}{\sqrt{2}}\)<=> \(x^2+y^2-2y+1=\frac{9}{4}\) (1)
\(\left|\overrightarrow{IB}\right|=\sqrt{\left(2-x\right)^2+\left(-2-y\right)^2}=\frac{3}{\sqrt{2}}\)<=> \(4-4x+x^2+4+8y+4y^2=\frac{9}{4}\) (2)
giải 1 và 2 ra được tọa độ I(x,y)
=> PTĐT: khi biết bán kính và tâm