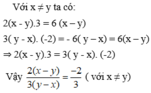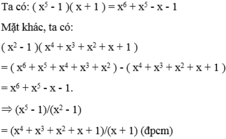Chứng minh các đẳng thức sau: ( x 3 - 1 ) ( x - 1 ) = x 2 + x + 1

Những câu hỏi liên quan
chứng minh các đẳng thức sau:
x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1
x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1
<=> x^5 - 1 = (x - 1)(x^4 + x^3 + x^2 + x + 1)
<=> x^5 - 1 = x^5 + x^4 + x^3 + x^2 + x - x^4 - x^3 - x^2 - x - 1
<=> x^5 - 1 = x^5 - 1 (đúng)
=> đpcm
bài 1 chứng minh các đẳng thức sau
\(\dfrac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}=\dfrac{1}{x-y}\)
\(VT=\dfrac{x^2+xy+2xy+2y^2}{x^2\left(x+2y\right)-y^2\left(x+2y\right)}=\dfrac{\left(x+y\right)\left(x+2y\right)}{\left(x+2y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}\)
Đúng 1
Bình luận (0)
Chứng minh các đẳng thức sau: 2 ( x - y ) 3 ( y - x ) = - 2 3 ( v ớ i x ≠ y )
Chứng minh các bất đẳng thức sau: \(\dfrac{x^2+1}{x}\ge2\)
BĐT này sai nha bạn.
Nó chỉ đúng khi \(x>0\)
Đúng 1
Bình luận (1)
Với \(x>0\) thì bất đẳng thức tương đương với \(x^2+1\ge2x\)
\(\Leftrightarrow x^2-2x+1\ge0\) \(\Leftrightarrow\left(x-1\right)^2\ge0\) (luôn đúng)
\(\Rightarrow\) Điều cần chứng minh là đúng
Đúng 2
Bình luận (0)
Chứng minh các đẳng thức sau:
(
x
5
-
1
)
(
x
2
-
1
)
(
x
4
+
x
3
+
x
2...
Đọc tiếp
Chứng minh các đẳng thức sau: ( x 5 - 1 ) ( x 2 - 1 ) = ( x 4 + x 3 + x 2 + x + 1 ) ( x + 1 )
Chứng minh các bất đẳng thức sau:
1
+
1
2
x
-
x
2
8
1
+
x
1
+
1
2...
Đọc tiếp
Chứng minh các bất đẳng thức sau:
1 + 1 2 x - x 2 8 < 1 + x < 1 + 1 2 x
với 0 < x < + ∞
Xét hàm số h(x) trên [0; + ∞ )
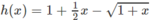
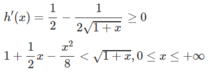
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
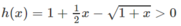
Hay
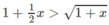
Xét hàm số trên f(x) trên [0; + ∞ );
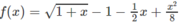
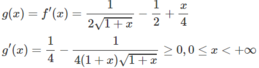
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
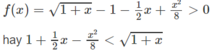
Với mọi 0 < x < + ∞
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau: \(\dfrac{x^2+1}{x}\ge2\left(x\ne0\right)\)
\(\dfrac{x^2+1}{x}=\dfrac{x^2}{x}+\dfrac{1}{x}=x+\dfrac{1}{x}\)
Theo bất đẳng thức Cô - si, ta có:
\(x+\dfrac{1}{x}\ge2\sqrt{x.\dfrac{1}{x}}=2\sqrt{1}=2\)
Vậy \(\dfrac{x^2+1}{x}\ge2\)
Đúng 4
Bình luận (0)
1 cách chứng minh khác (chứng minh tương đương)
\(\dfrac{x^2+1}{x}\ge2\\ \Leftrightarrow x^2+1\ge2x\\ \Leftrightarrow x^2-2x+1=\left(x-1\right)^2\ge0\left(\text{luôn đúng}\right)\)
Vậy BĐT ban đầu được chứng minh
Đúng 3
Bình luận (0)
chứng minh các đẳng thức sau (x-y)^3 +4y(2x^2+y^2)=(x+y)^3+2y(x^2+y^2)
\(\left(x-y\right)^3+4y\left(2x^2+y^2\right)=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
\(\Leftrightarrow x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(\Leftrightarrow\left(-3x^2y+8x^2y\right)+3xy^2+3y^3=\left(3x^2y+2x^2y\right)+3xy^2+3y^2\)
\(\Leftrightarrow5x^2y+3xy^2+3y^2=5x^2y+3xy^2+3y^2\)
Đúng 0
Bình luận (0)
Chứng minh các biểu thức sau ko phụ thuộc vào x :
A= (3x-2). ( 3x+2) - (3x+1) mũ 2 - 3.(-2x-1)
B= (x+1).(x-1) - (x-2) mũ 2 - 4.(x+3)
NẾU ĐC THÌ DÙNG CÁC HÀNG ĐẲNG THỨC Ạ
a) \(A=\left(3x-2\right)\left(3x+2\right)-\left(3x+1\right)^2-3.\left(-2x-1\right)\)
\(=\left(3x\right)^2-4-\left(9x^2+6x+1\right)+6x+3\)
\(=9x^2-4-9x^2-6x-1+6x+3\)
\(=-2\) không phụ thuộc vào x
b) \(B=\left(x+1\right)\left(x-1\right)-\left(x-2\right)^2-4.\left(x+3\right)\)
\(=x^2-1-\left(x^2-4x+4\right)-\left(4x+12\right)\)
\(=x^2-1-x^2+4x-4-4x-12\)
\(=-17\)không phụ thuộc vào x.