Chọn D.

Vì 30⁰ và 60⁰  là hai góc phụ nhau nên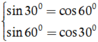 

Do đó: P = cos30⁰.cos60⁰ - sin30⁰.sin60⁰ = cos30⁰.cos60⁰ - cos30⁰.cos60⁰ = 0.

Chọn C.

Dùng bảng giá trị lượng giác các góc đặc biệt ta có

1) A. 999.

2) C. 9.

1: A

2: C

Câu 1: A

Câu 2: C

Chọn A

Bài 5: 

a: Thay \(x=4+2\sqrt{3}\) vào E, ta được:

\(E=\dfrac{\sqrt{3}+1-1}{\sqrt{3}+1-3}=\dfrac{\sqrt{3}}{\sqrt{3}-2}=-3-2\sqrt{3}\)

b: Để E<1 thì E-1<0

\(\Leftrightarrow\dfrac{\sqrt{x}-1-\sqrt{x}+3}{\sqrt{x}-3}< 0\)

\(\Leftrightarrow\sqrt{x}-3< 0\)

hay x<9

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 9\\x\ne1\end{matrix}\right.\)

c: Để E nguyên thì \(4⋮\sqrt{x}-3\)

\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;1;2;4\right\}\)

\(\Leftrightarrow\sqrt{x}\in\left\{4;5;7\right\}\)

hay \(x\in\left\{16;25;49\right\}\)

Câu 2:
a) Ta có \(x=4-2\sqrt{3}\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-2\right)^2}=\sqrt{3}-2\)

Thay \(x=\sqrt{3}-1\) vào \(B\), ta được

\(B=\dfrac{\sqrt{3}-1-2}{\sqrt{3}-1+1}=\dfrac{\sqrt{3}-3}{\sqrt{3}}=1-\sqrt{3}\)

b) Để \(B\) âm thì \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< 0\) mà \(\sqrt{x}+1\ge1>0\forall x\) \(\Rightarrow\sqrt{x}-2< 0\Rightarrow\sqrt{x}< 2\Rightarrow x< 4\)

c) Ta có \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=1-\dfrac{3}{\sqrt{x}+1}\)

Với mọi \(x\ge0\) thì \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+1\ge1\Rightarrow\dfrac{3}{\sqrt{x}+1}\le3\Rightarrow B=1-\dfrac{3}{\sqrt{x}+1}\ge-2\)

Dấu "=" xảy ra khi \(\sqrt{x}+1=1\Leftrightarrow x=0\)

Vậy \(B_{min}=-2\) khi \(x=0\)

bạn viết thế này khó nhìn quá

nhìn hơi đau mắt nhá bạn hoa mắt quá

1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)

\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)

Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)

                                                      \(\left(x+2\right)\ne0\Rightarrow x\ne-2\)

                                                      \(\left(x-2\right)\ne0\Rightarrow x\ne2\)

                         Vậy để biểu thức xác định thì : \(x\ne\pm2\)

b) để C=0 thì ....

1, c , bn Nguyễn Hữu Triết chưa lm xong 

ta có : \(/x-5/=2\)

\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)

thay x = 7  vào biểu thứcC

\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...

thay x = 3 vào C 

\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)

=> ko tìm đc giá trị C tại x = 3

chết mk nhìn nhầm phần c bài 2 :

\(2,\left(\frac{2+x}{2-x}+\frac{4x^2}{x^2-4}-\frac{2-x}{2+x}\right):\frac{x^2-3x}{2x^2-x^3}\)

Để P xác định 

\(\Rightarrow2-x\ne0\Rightarrow x\ne2\)

\(2+x\ne0\Rightarrow x\ne-2\)

\(x^2-4\ne0\Rightarrow x\ne0\)

\(x^2-3x\ne0\Rightarrow x\ne3\)

b, \(P=\left(\frac{2+x}{2-x}+\frac{4x^2}{\left(2+x\right)\left(2-x\right)}+\frac{2-x}{2+x}\right):\frac{x\left(x-3\right)}{x^2\left(2-x\right)}\)

\(P=\left[\frac{4+4x+x^2}{\left(2-x\right)\left(2+x\right)}-\frac{4x^2}{\left(2+x\right)\left(2-x\right)}-\frac{4-4x+x^2}{\left(2+x\right)\left(2-x\right)}\right].\frac{x\left(2-x\right)}{x-3}\)

\(P=\left[\frac{8x-4x^2}{\left(2-x\right)\left(2+x\right)}\right].\frac{x\left(2-x\right)}{x-3}=\frac{4x\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}.\frac{x\left(2-x\right)}{x-3}\)

\(P=\frac{4x^2\left(2-x\right)}{\left(x-3\right)\left(2+x\right)}\)

d, ĐỂ \(p=\frac{8x^2-4x^3}{x^2-x-6}< 0\)

\(TH1:8x^2-4x^3< 0\)

\(\Rightarrow8x^2< 4x^3\)

\(\Rightarrow2< x\Rightarrow x>2\)

\(TH2:x^2-x-6< 0\Rightarrow x^2< x+6\)