Chọn D.
Vì 300 và 600 là hai góc phụ nhau nên 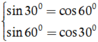
Do đó: P = cos300.cos600 - sin300.sin600 = cos300.cos600 - cos300.cos600 = 0.
Chọn D.
Vì 300 và 600 là hai góc phụ nhau nên 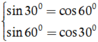
Do đó: P = cos300.cos600 - sin300.sin600 = cos300.cos600 - cos300.cos600 = 0.
Tính giá trị biểu thức P = sin300.cos600 + cos300.sin600
A. 1
B. 0
C. 2
D. 3
Giá trị của cos300 + sin600 bằng bao nhiêu?
A. 3 3
B. 3 2
C. 3
D. 1.
câu20:Cho tana=-2 và pi/2<a<pi.Tính giá trị biểu thức P=cos2a+sin2a
câu21Cho 2tana-cota=1 và -pi/2<a<0.Tính giá trị của biểu thức P=tana+2cota
câu22: Cho sina=-1/7 và pi<a<3pi/2.Tính giá trị của biểu thức P=cos(a+pi/6)
câu23: Cho sina=-1/9; cosb=-2/3 và pi<a<3pi/2; pi/2<b<pi. Tính giá trị của biểu thức P= sin(a+b)
biểu thức P = 3|x - 2| + |3x + 1| đạt giá trị nhỏ nhất tại mọi x trên đoạn [b;a]. Tính giá trị của biểu thức S = 3b + 2a
Cho hàm số \(f\left(x\right)\) là hàm số bậc hai với hệ số \(a>0\), thỏa mãn \(\left|f\left(x\right)\right|\le1,\forall x\in\left[-1;1\right]\) và biểu thức \(P=\dfrac{8}{3}a^2+2b^2\) đạt giá trị lớn nhất. Tính giá trị của biểu thức \(Q=5a+11b+c.\)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại B với A(1;-1), C(3;5). Điểm B nằm trên đường thẳng d: 2x - y = 0. Phương trình các đường thẳng AB, BC lần lượt là ax + by - 24 = 0, cx + dy + 8 = 0. Tính giá trị biểu thức a.b.c.d.
cho cosα=\(\dfrac{3}{5}\)(0<α<\(\dfrac{\pi}{2}\))
a. Tính sinα.
b. Tính giá trị biểu thức P=cos2α-cosα.
Cho các số thực a. b, c, d thỏa mãn a^2 + b^2 - 2a +4b + 1 = 0 và 2c - d + 1 = 0. tìm giá trị nhỏ nhất của biêu thức P= (a-c)^2 + (b-d)^2
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), trọng tâm G ( 2 ; 2 3 ) . Biết rằng đỉnh B nằm trên đường thẳng d: x + y + 2 = 0 và đỉnh C có hình chiếu vuông góc trên d là điểm H(2;-4). Giả sử B(a;b). Tính giá trị của biểu thức P = a - 3b.