Với giá trị nào của m thì ba đường thẳng phân biệt d 1 : y = ( m + 2 ) x – 3 m − 3 ; d 2 : y = x + 2 v à d 3 : y = m x + 2 giao nhau tại một điểm?
A. m = 1 3
B. m = - 5 3
C. m = 1 ; m = − 5 3 ;
D. m = − 5 6
Với giá trị nào của m thì ba đường thẳng phân biệt 3x + 2y = 4; 2x – y = m; x + 2y = 3 đồng quy
\(3x+2y=4\Leftrightarrow2y=4-3x\Leftrightarrow y=-\dfrac{3}{2}x+2\\ x+2y=3\Leftrightarrow2y=3-x\Leftrightarrow y=-\dfrac{1}{2}x+\dfrac{3}{2}\)
PT hoành độ giao điểm 2 đt trên là \(-\dfrac{3}{2}x+2=-\dfrac{1}{2}x+\dfrac{3}{2}\Leftrightarrow x=\dfrac{7}{2}\Leftrightarrow y=-\dfrac{13}{4}\Leftrightarrow A\left(\dfrac{7}{2};-\dfrac{13}{4}\right)\)
Để 3 đt đồng quy thì \(A\left(\dfrac{7}{2};-\dfrac{13}{4}\right)\in2x-y=m\)
\(\Leftrightarrow m=2\cdot\dfrac{7}{2}+\dfrac{13}{4}=\dfrac{41}{4}\)
Cho hàm số y = f x = x 3 − 3 x 2 + 1 (C) đồ thị như hình vẽ bên. Với giá trị nào của m thì đường thẳng y = m + 1 cắt (C) tại ba điểm phân biệt có hoành độ x 1 < 1 < x 2 < x 3 ?
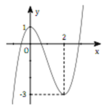
A. − 4 < m < 0.
B. − 2 < m < 0.
C. − 4 < m < − 2.
D. m = − 2.
Đáp án C
Em có f(1) = -1. Do đường thẳng y = m +1 có đồ thị là một đường thẳng song song hoặc trùng với trục hoành. Vậy để đường thẳng y = m +1 cắt (C) tại ba điểm phân biệt có hoành độ x 1 < 1 < x 2 < x 3 thì đường thẳng y = m +1 phải cắt đồ thị như hình vẽ
⇔ − 3 < m + 1 < − 1 ⇔ − 4 < m < − 2
Cho hàm số y = 2 x + 3 x + 2 có đồ thị (C) và đường thẳng d ; y = x + m. Với giá trị nào của tham số m thì d cắt (C) tại hai điểm phân biệt?
A. m < -2
B. m < 2 hoặc m > 6
C. 2 < m < 6
D. m < -6
Đáp án B
2 x + 3 x + 2 = x + m ⇔ 2 x + 3 = x 2 + m x + 2 x + 2 m ⇔ f x = x 2 + m x + 2 m - 3 = 0 ( 1 )
Rõ ràng f - 2 ≠ 0 , ∀ m nên ta cần có ∆ > 0 ⇔ m 2 - 4 2 m - 3 > 0 ⇔ [ m > 6 m < 2 .
Cho đường thẳng y=(m-2)x + m (d)
a) Với giá trị nào của m thì đường thẳng (d) đi qua gốc tọa độ?
b) Với giá trị nào của m thì đường thẳng (d) đi qua điểm A(2;5)
c) Với giá trị nào của m thì đường thẳng (d) cắt đường thẳng y = 3x - 2
Cho parabol (P): y=x và đường thẳng (d): y =2mx−m’ +2m+1 a) Vẽ (P). b) Với giá trị nào của m thì (P) và (d) cắt nhau tại hai điểm phân biệt cùng nằm bên phải trục tung.
Cho hai đường thẳng d: y= x+ 2m và d’: y= 3x+2 ( m là tham số). Có mấy giá trị của m để ba đường thẳng d; d’ và d’’: y= -mx+ 2 phân biệt đồng quy.
A.0
B. 1
C. 2
D. 3
Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
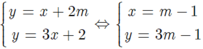
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.
giá trị nào của m thì đường thẳng (d) y=3/2x+2m cắt (p) y=-3/4x2 tại 2 điểm phân biệt
Trong mặt phẳng tọa độ Oxy, cho Parabol (P):\(y=x^2\) và đường thẳng (d): y=2(m+3)x+1-4m (m là tham số). Với giá trị nào của m thì (d) cắt (P) tại 2 điểm phân biệt cùng nằm bên phải trục tung
xét phương trình hoành độ giao điểm của ( p ) vả ( d )
\(x^2=2\left(m+3\right)x+1-4m\)
\(< =>x^2-2\left(m+3\right)x-1+4m=0\)
ta có : ( \(a=1;b=2\left(m+3\right);b'=m+3;c=-1+4m\) )
\(\Delta'=b'^2-ac\)
\(\Delta'=\left(m+3\right)^2-1.\left(-1+4m\right)\)
\(\Delta'=m^2+2m3+3^2+1-4m\)
\(\Delta'=m^2+6m+9+1-4m\)
\(\Delta'=m^2+6m-4m+1+9\)
\(\Delta'=\left(m^2+2m.1+1^2\right)+9\)
\(\Delta'=\left(m+1\right)^2+9>0;\forall m\)
Vay : với mọi m thì (đ) cắt (đ) tại 2 điểm phân biệt cùng nằm bên phải trục tung
CHÚ Ý : NẾU BẠN LẤY \(\Delta'\)> 0 rồi tìm tham số m ( là sai nha )
vì : bất kỳ m là số nào thì ( đ) cũng luôn cắt ( đ) tại 2 điểm phân biệt bên phải trục tung
( m không thuộc riêng về 1 giá trị nào hết nha )
OK CHÚC BẠN HỌC TỐT !!!!
Hàm số y = x 3 + 3 x 2 - 2 Với các giá trị nào của m thì đồ
thị hàm số cắt đường thẳng d : y = m tại 3 điểm phân
biệt?`
A. - 2 < m < 0
B. 0 < m < 2
C. - 2 < m < 2
D. m < - 2 ∨ m > 2