Không sử dụng máy tính, hãy chứng minh:
Những câu hỏi liên quan
21 tháng 10 2021 lúc 21:30
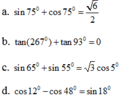
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
Không sử dụng máy tính, hãy tính: log 2 1 8
Không sử dụng máy tính, hãy tính: log 0 , 5 0 , 125
Không sử dụng máy tính, hãy tính: log 3 3 4
Không sử dụng máy tính, hãy tính: log 1 4 2
SGK Chân trời sáng tạo - Trang 7
25 tháng 7 2023 lúc 21:52
Hãy trao đổi với bạn về một tình huống máy tính bị lỗi, hỏng do sử dụng không đúng cách mà em đã chứng kiến hoặc nghe kể lại.
Bị đơ máy tính do bị virus, bị hỏng màn, bị rơi máy,...
Đúng 0
Bình luận (0)
không sử dụng máy tính, chứng minh \(Q=\sqrt{2014^2+2014^2.2015^2+2015^2}\)là số nguyên
Một cách khác nhé!
Đặt a=2014, b=2015 => b-a=1
Khi đó: \(Q=\sqrt{a^2+a^2b^2+b^2}=\sqrt{\left(b-a\right)^2+a^2b^2+2ab}=\sqrt{a^2b^2+2ab+1}=\sqrt{\left(ab+1\right)^2}\)
\(=ab+1=2014.2015+1=4058211\)
Đúng 0
Bình luận (0)
Đặt \(2014=a\) thì ta có:
\(Q=\sqrt{a^2+a^2.\left(a+1\right)^2+\left(a+1\right)^2}\)
\(=\sqrt{a^4+2a^3+3a^2+2a+1}\)
\(=\sqrt{\left(a^2+a+1\right)^2}=a^2+a+1\)
Vậy Q là số nguyên
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Không sử dụng máy tính, hãy tính
sin
40
0
-
sin
45
0
+
sin
50
0
cos
40
0...
Đọc tiếp
Không sử dụng máy tính, hãy tính sin 40 0 - sin 45 0 + sin 50 0 cos 40 0 - cos 45 0 + cos 50 0 = 6 3 + 3 tan 15 ° 3 - 3 tan 15 °
Ta có: sin 40º = cos 50º ; sin 45º = cos 45º ; sin 50º = cos 40º
Do đó :
Đúng 0
Bình luận (0)
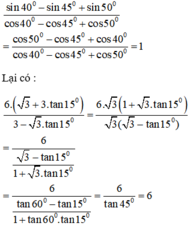
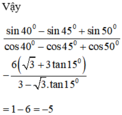
Không sử dụng máy tính. Hãy tính:
A=10101x[5/111111+5/222222-4/(3x7x11x13x37)]