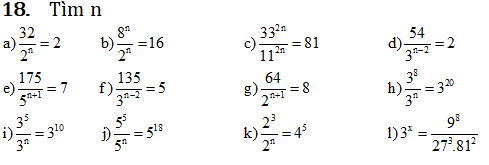
Giải nhớ nêu thêm các bước giải
giải giúp mình 1 + 3 + 5 ...+ x =225 . giải nhớ ghi rõ các bước tính luôn nha
1. nêu các bước để thêm tiêu đề cho biểu đồ
2. Nêu các bước để thêm tiêu đề trục đứng và trục ngang
4. Nếu các bước thêm hoặc ẩn chú giải
5. Nếu các bước để thay đổi vị trí và kích thước của biểu đồ
nêu các bước giải bài toán theo pthh
Hỏi a có song song với b ( nêu các bước giải)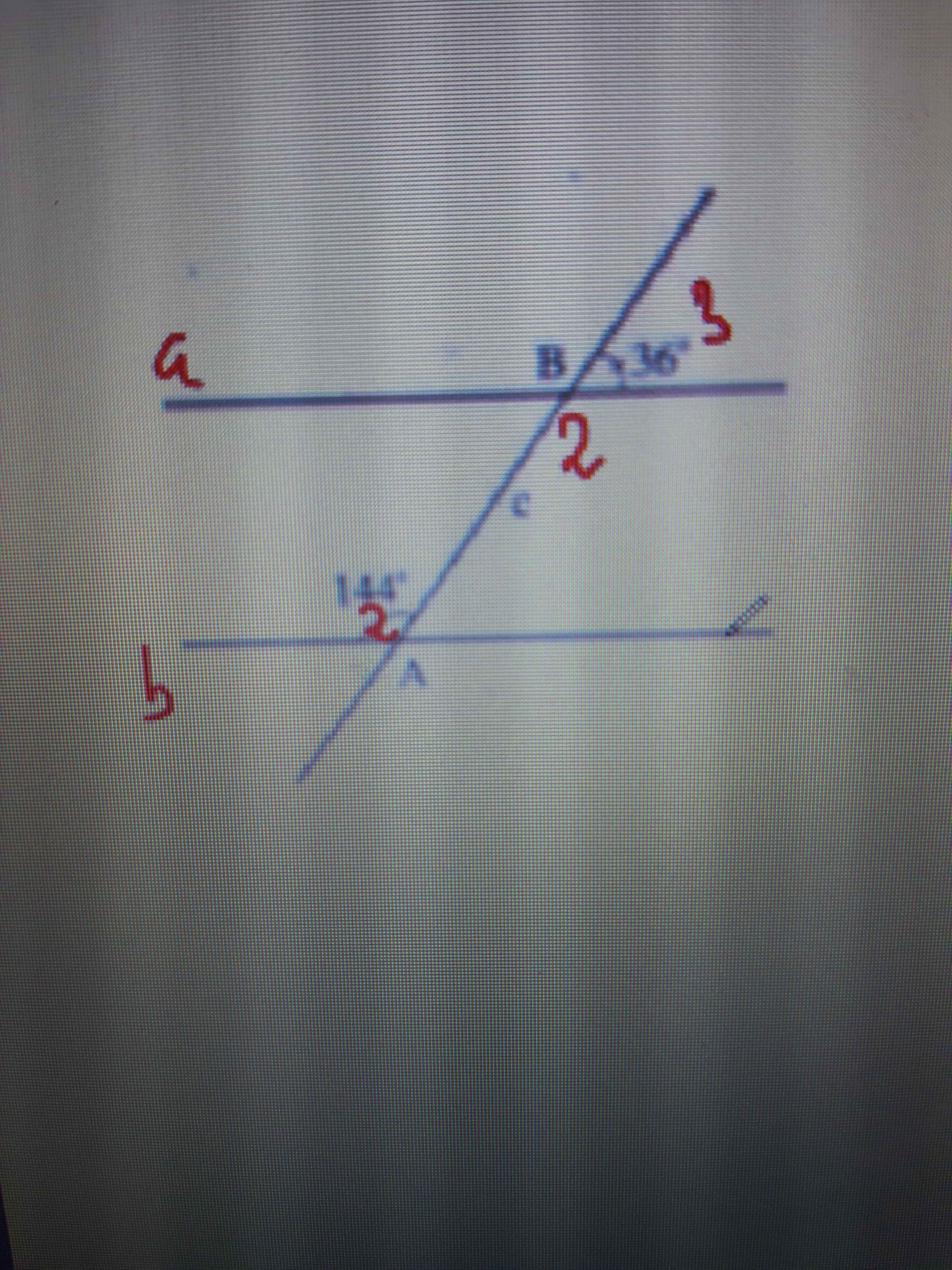
\(\widehat{B_3}+\widehat{B_2}=180^o\) (2 góc kề bù)
\(\Rightarrow\widehat{B_2}=180^o-\widehat{B_3}=180^o-36^o=144^o\)
Có \(\widehat{B_2}=\widehat{C_2}\left(=144^o\right)\)
Mà 2 góc ở vị trí so le trong
\(\Rightarrow a//b\) (dấu hiệu nhận biết)

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )
\(7,=\left(\sqrt{x}\right)^2+2\cdot2\sqrt{x}+2^2=\left(\sqrt{x}+2\right)^2\\ 8,=\left(\sqrt{x}\right)^2-2\cdot3\sqrt{x}+3^2=x-6\sqrt{x}+9\\ 9,=\sqrt{x^3}+\sqrt{y^3}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\\ 10,=\sqrt{x^3}-\sqrt{y^3}=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\\ 11,=\sqrt{x^3}+1^3=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\\ 12,=\sqrt{x^3}-2^3=\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)\)
7: \(x+4\sqrt{x}+4=\left(\sqrt{x}+2\right)^2\)
8: \(\left(\sqrt{x}-3\right)^2=x-6\sqrt{x}+9\)
9: \(x\sqrt{x}+y\sqrt{y}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )
7) \(x+4\sqrt{x}+4=\left(\sqrt{x}\right)^2+2\sqrt{x}.2+2^2=\left(\sqrt{x}+2\right)^2\)
8) \(\left(\sqrt{x}-3\right)^2=\left(\sqrt{x}\right)^2-2.\sqrt{x}.3+3^2=x-6\sqrt{x}+9\)
9) \(x\sqrt{x}+y\sqrt{y}=\sqrt{x^3}+\sqrt{y^3}=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)
10) \(x\sqrt{x}-y\sqrt{y}=\sqrt{x^3}-\sqrt{y^3}=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\)
11) \(x\sqrt{x}+1=\sqrt{x^3}+1^3=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
12) \(x\sqrt{x}-8=\sqrt{x^3}-2^3=\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)\)
7. x + \(4\sqrt{x}+4\)
= \(\left(\sqrt{x}\right)^2+2.2.\sqrt{x}+2^2\)
= \(\left(\sqrt{x}+2\right)^2\)

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )

dùng hằng đẳng thức biến đổi các đa thức sau ( nhớ giải chi tiết từng bước ra )
9) \(x-1=\left(\sqrt{x}\right)^2-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
10) \(x\sqrt{x}-1=\sqrt{x^3}-1=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)
11) \(x-2\sqrt{x}-63=\left(x-2\sqrt{x}+1\right)-64=\left(\sqrt{x}-1\right)^2-8^2=\left(\sqrt{x}-1-8\right)\left(\sqrt{x}-1+8\right)=\left(\sqrt{x}-9\right)\left(\sqrt{x}+7\right)\)