Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) có phương trình: x 2 + y 2 + 4 3 x - 4 = 0 Tia Oy cắt (C) tại A(0;2). Lập phương trình đường tròn (C’), bán kính R’= 2 và tiếp xúc ngoài với C tại A.
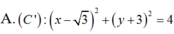
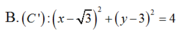
![]()
![]()
Trong mặt phẳng với hệ toạ độ Oxy cho đường tròn C có phương trình: x^2+y^2-4x+8y-5=0. Viết ptrinh đường thẳng vuông góc với đường thẳng d:3x-4y+12=0 và cắt đường tròn C theo một dây cung có độ dài bằng 8
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A (-1;1) và đường thẳng
d : x - y + 1 - √2 = 0 . Viết phương trình đường tròn (C) đi qua điểm A, gốc toạ độ O và tiếp xúc với đường thẳng d .
Trong mặt phẳng với hệ tọa độ Oxy, cho điểm A (-1;1) và đường thẳng
d : x - y + 1 - √2 = 0 . Viết phương trình đường tròn (C) đi qua điểm A, gốc toạ độ O và tiếp xúc với đường thẳng d .
Gọi \(I\) là tâm nằm trên đường trung trực \(OA\)
\(\Rightarrow IA=d\left(I,d\right)\Leftrightarrow\sqrt{\left(x_0+1\right)^2+x^2_0}=\dfrac{\left|-x_0+x_0+1-1\right|}{\sqrt{2}}\Leftrightarrow\left[{}\begin{matrix}x_0=0\\x_0=-1\end{matrix}\right.\)
Khi đó: \(\left\{{}\begin{matrix}x_0=0\Rightarrow r=1\\x_0=-1\Rightarrow r=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2+\left(y-1\right)^2=1\\\left(x+1\right)^2+y^2=1\end{matrix}\right.\)
Bài 1: Trong mặt phẳng với hệ toạ độ Đềcác vuông góc Oxy, cho đường thẳng (∆): 2x+y+3=0 và hai điểm A(-5;1), B(-2;4) 1. Viết phương trình đường tròn C đi qua A,B và có tâm I∈ (∆). 2. Viết phương trình đường tiếp tuyến tại A với đường tròn C. 3. Viết phương trình các tiếp tuyến với (C), biết tiếp tuyến đi qua D(1;2). Tìm toạ độ tiếp điểm. Bài 2: Trong mặt phẳng với hệ toạ độ Oxy cho điểm I(-2;1) và đường thẳng d: 3x-4y=0 a. Viết phương trình đường tròn (C) có tâm I và tiếp xúc với đường thẳng d. b. Viết phương trình tập hợp các điểm mà qua các điểm đó vẽ được hai tiếp tuyến đến (C) sao cho hai tiếp tuyến vuông góc với nhau.
Bài 2:
a: \(R=d\left(I;d\right)=\dfrac{\left|-2\cdot3+1\cdot\left(-4\right)\right|}{\sqrt{3^2+\left(-4\right)^2}}=2\)
Phương trình (C) là:
(x+2)^2+(y-1)^2=2^2=4
Bài 1:
a: I thuộc Δ nên I(x;-2x-3)
IA=IB
=>IA^2=IB^2
=>\(\left(x+5\right)^2+\left(-2x-3-1\right)^2=\left(x+2\right)^2+\left(-2x-3-4\right)^2\)
=>x^2+10x+25+4x^2+16x+16=x^2+4x+4+4x^2+28x+49
=>26x+41=32x+53
=>-6x=-12
=>x=2
=>I(2;-7): R=IA=căn 113
Phương trình (C) là:
(x-2)^2+(y+7)^2=113
2: vecto IA=(7;-8)
Phương trình tiếp tuyến là:
7(x+5)+(-8)(y-1)=0
=>7x+35-8y+8=0
=>7x-8y+43=0
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): ( x + 1 ) 2 + ( y - 3 ) 2 = 4 . Phép tịnh tiến theo vectơ v → = 3 ; 2 biến đường tròn (C) thành đường tròn có phương trình nào dưới đây
A. ( x + 2 ) 2 + ( y + 5 ) 2 = 4
B. ( x - 1 ) 2 + ( y + 3 ) 2 = 4
C. ( x + 4 ) 2 + ( y - 1 ) 2 = 4
D. ( x - 2 ) 2 + ( y - 5 ) 2 = 4
Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) : x2 + y2 – 2x + 2y + 1 = 0
Phương trình đường tròn (C’) đối xứng (C) qua trục tung là:
A. ( x − 1 ) 2 + ( y − 1 ) 2 = 1
B. ( x + 1 ) 2 + ( y − 1 ) 2 = 2
C. ( x + 1 ) 2 + ( y + 1 ) 2 = 2
D. ( x + 1 ) 2 + ( x + 1 ) 2 = 1
Đáp án D
(C) có tâm I( 1; – 1), bán kính 1
Đ O y : I => I’( – 1; – 1 )
Phương trình đường tròn (C’): ( x + 1 ) 2 + ( y + 1 ) 2 = 1
Trong mặt phẳng Oxy , cho điểm I có tung độ dương và thuộc đường thẳng d:3x+y+4=0 . Phương trình đường tròn (C) có tâm I và tiếp xúc với các trục toạ độ là
a) \(\left(x+1\right)^{2^{ }}+\left(y+1\right)^{2^{ }}=2\)
b) \(\left(x+2\right)^{2^{ }}+\left(y-2\right)^{2^{ }}=4\)
c) \(\left(x-1\right)^{2^{ }}+\left(y-1\right)^{2^{ }}=2\)
d) \(\left(x-2\right)^{2^{ }}+\left(y+2\right)^{2^{ }}=4\)
I(x,y) có tung độ dương nên y>0 và thuộc (d)
nên I(x;-3x-4)
y>0
=>-3x-4>0
=>-3x>4
=>x<-4/3
Theo đề, ta có: d(I;Ox)=d(I;Oy)=R
(C) tiếp xúc với Ox,Oy nên |x|=|-3x-4|
=>3x+4=x hoặc -3x-4=x
=>2x=-4 hoặc -4x=4
=>x=-2(nhận) hoặc x=-1(loại)
=>I(-2;2)
R=|2|=2
=>(C): (x+2)^2+(y-2)^2=4
=>B
Trong mặt phẳng Oxy , cho điểm I có tung độ dương và thuộc đường thẳng d:3x+y+4=0 . Phương trình đường tròn (C) có tâm I và tiếp xúc với các trục toạ độ là
a) \(\left(x+1\right)^{2^{ }}+\left(y+1\right)^{2^{ }}=2\)
b) \(\left(x+2\right)^{2^{ }}+\left(y-2\right)^{2^{ }}=4\)
c) \(\left(x-1\right)^{2^{ }}+\left(y-1\right)^{2^{ }}=2\)
d) \(\left(x-2\right)^{2^{ }}+\left(y+2\right)^{2^{ }}=4\)
I(x,y) có tung độ dương nên y>0 và thuộc (d)
nên I(x;-3x-4)
y>0
=>-3x-4>0
=>-3x>4
=>x<-4/3
Theo đề, ta có: d(I;Ox)=d(I;Oy)=R
(C) tiếp xúc với Ox,Oy nên |x|=|-3x-4|
=>3x+4=x hoặc -3x-4=x
=>2x=-4 hoặc -4x=4
=>x=-2(nhận) hoặc x=-1(loại)
=>I(-2;2)
R=|2|=2
=>(C): (x+2)^2+(y-2)^2=4
=>B