Cho hình chóp S.ABCD có SA vuông góc với (ABC), AB=a, AC= a 2 , BAC= 45 o Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên SA, SC Tính thể tích mặt cầu ngoại tiếp hình chóp A.BC C 1 B 1 .
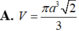
![]()
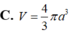
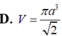
Cho hình chóp S.ABC có SA vuông góc với (ABC), AB=a, AC=a 2 , B A C ^ = 45 ° . Gọi B',C' lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A.BCC'B'.
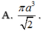
![]()
![]()
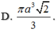
Cho hình chóp S.ABC có SA vuông góc với A B C , A B = a ; A C = a 2 , B A C ⏜ = 45 ° . Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên S B , S C . Tính thể tích mặt cầu ngoại tiếp hình chóp A . B C C 1 B 1 .
A. V = π a 3 2 3
B. V = π a 3 2
C. V = 4 3 π a 3
D. V = π a 3 2
Đáp án A
Dễ thấy Δ A B C là tam giác vuông cân tại B, do đó O A = O B = O C (với O là trung điểm của AC)
Ta có B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ A B 1 , lại do A B 1 ⊥ S B ⇒ A B 1 ⊥ B 1 C
Do đó Δ A B 1 C vuông tại O nên O A = O C = O B 1
Vậy O là tâm mặt cầu ngoại tiếp hình chóp A B C C 1 B 1
Do đó R = A C 2 = a 2 2 ⇒ V = 4 3 π R 3 = π a 3 2 3
Cho hình chóp S.ABCD có đáy ABC là tam giác với AB=2 cm, AC=3cm, ∠ B A C = 60 ° , S A ⊥ ( A B C ) . Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối cầu đi qua năm điểm A, B, C, B 1 , C 1
A. 28 21 π 27 c m 3
B. 76 57 π 27 c m 3
C. 7 7 π 6 c m 3
D. 27 π 6 c m 3
Chọn A.
Phương pháp:
Xác định tâm, bán kính của khối cầu.
Thể tích khối cầu có bán kính r là:
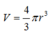
Cách giải:
Gọi O là tâm đường tròn ngoại tiếp
DABC, đường kính AD.
Ta chứng minh O là tâm mặt cầu đi qua 6 điểm A, B, C, B 1 , C 1 và D
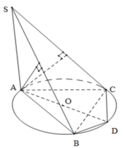

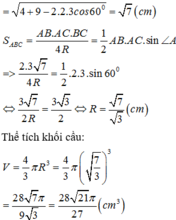
Cho hình chóp S.ABCD có đáy ABC là tam giác với AB=2cm,AC=3cm, B A C ^ = 60 0 . S A ⊥ ( A B C ) . Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối cầu đi qua năm điểm A,B,C, B 1 , C 1
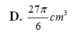
Cho hình chóp S.ABC có SA vuông góc với A B C , A B = a ; C A = a 2 ; B A C = 45 ° . Gọi B 1 ; C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích mặt cầu ngoại tiếp hình chóp A . B C C 1 B 1
A. V = π a 3 2 3
B. V = π a 3 2
C. V = 4 3 π a 3
D. V = π a 3 2
Đáp án A
Công thức
R = B C 2 sin B A C ⏜ = a 2 + 2 a 2 − 2 a . a 2 cos 45 ° 2 sin 45 ° = a 2 ⇒ V = 4 3 π R 3 = π a 3 2 3
Cho hình chóp S.ABC có SA vuông góc với (ABC), A B = a ; A C = a 2 , B A C ^ = 45 o . Gọi lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C C 1 B 1 bằng
A. π a 3 2 .
B. π a 3 2 .
C. 4 3 π a 3 .
D. π a 3 2 3 .
Cho hình chóp S.ABC có SA vuông góc với (ABC), A B = a ; A C = a 2 ; B A C ^ = 45 o .Gọi B 1 ; C 1 lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C C 1 B 1 bằng
A. πa 3 2
B. πa 3 2
C. 4 3 πa 3
D. πa 3 2 3
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB = α . Áp dụng: Tính VS ABCD . trong trường hợp α = 60 độ.
Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC =120độ . Cho SA vuông góc với đáy và SC = 2a .Tính thể tích hình chóp S.ABCD.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC=20 cm BC=15 cm AB=25 cm . Cho SA vuông góc với đáy và SA =18cm . Tính thể tích của khối chóp.
Bài 9. Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt bên SBC là tam giác đều cạnh a. Cho gócBAC =120 . Tính VS ABC .
. Bài 10. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB= BC= a . Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác S.ABC:
a.Tính thể tích khối chóp S.ABC
b.Chứng minh SC vuông góc với (AB'C')
c.Tính thể tích khối chóp S.ABC
Cho hình chóp S.ABCD có đáy là tam giác vuông cân tại B. SA vuông góc với đáy. SA = a căn 3. AC = a căn 2 a) Tính góc giữa đt SB và (ABC) b) Tính góc giữa đt AC và (SBC) c) Tính gics giữa đt BC và (SAC) d) Tính góc giữa đt SB và (BAC) e) Tính góc giữa đt SC và (SAB)
a: (SB;(ABC))=(BS;BA)=góc SBA
BA^2+BC^2=AC^2
=>2*BA^2=AC^2
=>AB=BC=a
tan SBA=SA/SB=căn 3
=>góc SBA=60 độ
d: (SB;(BAC))=(BS;BA)=góc SBA=60 độ
e:
CB vuông góc AB
CB vuông góc SA
=>CB vuông góc (SBA)
=>(SC;(SBA))=(SC;SB)=góc BSC
SB=căn SA^2+AB^2=2a
SC=căn SA^2+AC^2=a*căn 5
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
sin BSC=BC/SC=a/a*căn 5=1/căn 5
=>góc BSC\(\simeq27^0\)