Chọn A.
Phương pháp:
Xác định tâm, bán kính của khối cầu.
Thể tích khối cầu có bán kính r là:
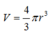
Cách giải:
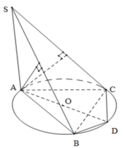
Gọi O là tâm đường tròn ngoại tiếp
DABC, đường kính AD.
Ta chứng minh O là tâm mặt cầu đi qua 6 điểm A, B, C, B 1 , C 1 và D

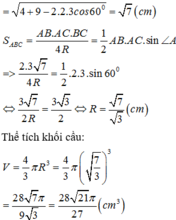
Chọn A.
Phương pháp:
Xác định tâm, bán kính của khối cầu.
Thể tích khối cầu có bán kính r là:
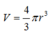
Cách giải:
Gọi O là tâm đường tròn ngoại tiếp
DABC, đường kính AD.
Ta chứng minh O là tâm mặt cầu đi qua 6 điểm A, B, C, B 1 , C 1 và D


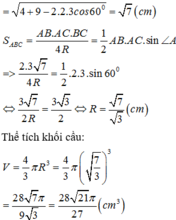
Cho hình chóp S.ABC có ABC là tam giác mà A B = 1 , A C = 2 , B A C ^ = 60 ∘ ; SA vuông góc với mặt phẳng (ABC). Gọi B 1 , C 1 là hình chiếu của A lên SB, SC. Tính diện tích mặt cầu đi qua bốn đỉnh A , B , C , B 1 , C 1 ?
A. 8 π
B. 4 π
C. 16 π
D. 12 π
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A, B, C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính bán kính mặt cầu đi qua năm điểm A,B,C, B 1 , C 1 .
A. a 3 2
B. a 3 3
C. a 3 4
D. a 3 6
Cho hình chóp S.ABC có S A ⊥ ( A B C ) , A B = 1 , A C = 2 , B A C ^ = 60 ° Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu đi qua các điểm A,B,C,M,N
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có SA ^ (ABC), AB = 1, AC = 2 và B A C ⏜ = 60 ° . Gọi M , N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu đi qua các điểm A, B, C, M, N
A. R = 2
B. R = 2 3 3
C. R = 4 3
D. R = 1
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi B 1 , C 1 lần lượt là hình chiếu của A trên SB, SC. Tính theo a bán kính R của mặt cầu đi qua năm điểm A , B , C , B 1 , C 1
A. R = a 3 6
B. R = a 3 2
C. R = a 3 6
D. R = a 3 6
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy S A = a 2 . Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Tính thể tích hình chóp S.AB′C′.
A. a 3 2
B. a 3 6
C. a 3 24
D. a 3 12
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, S A = S B = S C = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
A. a 3 3
B. a 3
C. a 3 24
D. a 3 12