Đáp án C
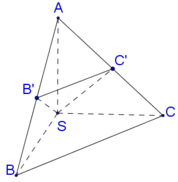
Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
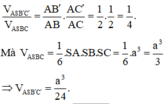
Đáp án C

Vì SA=SB=SC suy ra tam giác SAB và tam giác SAC cân tại S. Vậy B′,C′ lần lượt là trung điểm của AB,AC.
Ta có:
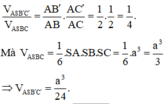
Cho hình chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥ SA ; SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB, AC. Thể tích của hình chóp S.AB′C′ là
A. a 3 24
B. a 3
C. a 3 3
D. a 3 12
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a . Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Tính thể tích hình chóp S.AB′C′.
A. a 3 2
B. a 3 6
C. a 3 24
D. a 3 12
Cho hình chóp S.ABC có SA vuông góc với (ABC), A B = a ; A C = a 2 , B A C ^ = 45 o . Gọi lần lượt là hình chiếu vuông góc của A lên SB, SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C C 1 B 1 bằng
A. π a 3 2 .
B. π a 3 2 .
C. 4 3 π a 3 .
D. π a 3 2 3 .
Cho hình chóp S.ABC có S A = a , A B = a 3 , B A C ^ = 150 ° và SA vuông góc với mặt phẳng đáy. Gọi M, N lần lượt là hình chiếu vuông góc của A trên SB và SC. Thể tích khối cầu ngoại tiếp hình chóp A.BCMN bằng
A. 4 7 π a 3 3
B. 44 11 π a 3 3
C. 28 7 π a 3 3
D. 20 5 π a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a. Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN
A. V = a 3 36
B. V = a 3 5 15
C. V = a 3 3 18
D. V = a 3 30
Cho hình chóp S.ABC có SC = 2a và S C ⊥ A B C , ∆ A B C vuông cân tại B , A B = 2 a Gọi D, E lần lượt là hình chiếu vuông góc của C lên SA, SB. Thể tích khối chóp S.CDE bằng
A. 4 a 3 9
B. 2 a 3 3
C. 2 a 3 9
D. a 3 3
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy S A = a 2 . Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và S A = S B = S C = a . Tính thể tích của khối chóp S. ABC.
A. 1 3 a 3
B. 1 2 a 3
C. 1 6 a 3
D. 2 3 a 3
Cho hình chóp S.ABC có SA vuông góc với A B C , A B = a ; A C = a 2 , B A C ⏜ = 45 ° . Gọi B 1 , C 1 lần lượt là hình chiếu vuông góc của A lên S B , S C . Tính thể tích mặt cầu ngoại tiếp hình chóp A . B C C 1 B 1 .
A. V = π a 3 2 3
B. V = π a 3 2
C. V = 4 3 π a 3
D. V = π a 3 2