Tìm giá trị thực của m để hàm số F(x) = x³ – (2m – 3)² – 4x + 10 là một nguyên hàm của hàm số f(x) = 3x² – 12x – 4 với mọi  x ∈ ℝ

A.  m = 3 2

B.  m = - 9 2

C.  m = 9 2

D.  m = 9

Cho hàm số y = f(x) có bảng biến thiên như sau:

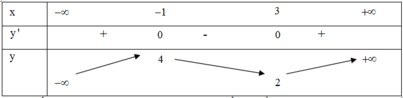
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m + 1 có 3 nghiệm thực phân biệt?

A. –3 ≤ m ≤ 3

B. –2 ≤ m ≤ 4

C. –2 < m < 4

D. –3 < m < 3

Cho hàm số y=f(x). Hàm số y=f' (x) có đồ thị như  hình bên.

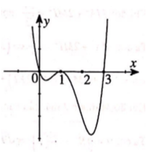
Tìm m để hàm số y = f ( x 2 + m ) có 3 điểm cực trị?

A. m ∈ [ 0 ; 3 ]   
m ∈ ( 3 ; + ∞ )    

m ∈ ( - ∞ ; 0 )

B. m ∈ [ 0 ; 3   )

C. m ∈ ( 3 ; + ∞ )    

D. m ∈ ( - ∞ ; 0 )

Cho hàm số f ( x ) thỏa mãn f ( t a n x ) = c o s 4 x . Tìm tất cả các số thực m để đồ thị hàm số  g ( x ) = 2019 f ( x ) - m có hai đường tiệm cận đứng

A. m < 0

B. 0 < m < 1

C. m > 0

D. m < 1

Cho hàm số f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tìm tất cả các giá trị thực của tham số m để hàm số y=f(|x|) có 5 cực trị

A.  - 10 < m < 5 4

B.  - 2 < m < 5

C.  - 2 < m < 5 4

D.  5 4 < m < 2